Chantry09
- 59
- 0
Hi,
Im trying to work out the dimensions of the offset on a cam for a project. I know the travel of rod c, as well as the length of the connecting rod b, but I am not sure what the lenth of dimension a should be. I know this is probably simple maths (just pythagoras?) but I need to make sure I get the full travel out of rod c with full 360 degree rotation on the axel.
It would normally be very simple (a = 0.5 x travel of rod c), but it is the fact that rod b is allowed to pivot around the joint to rod c makes it a bit more confusing.
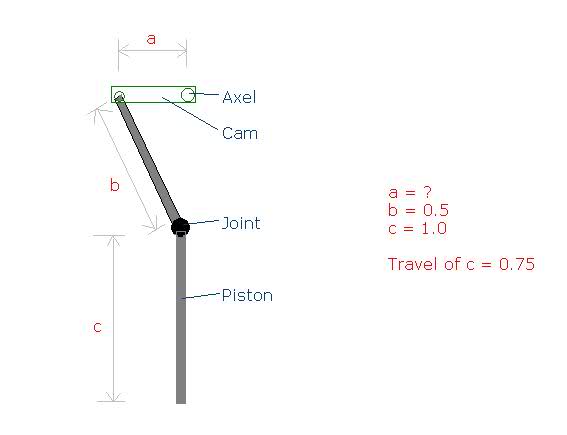
Im trying to work out the dimensions of the offset on a cam for a project. I know the travel of rod c, as well as the length of the connecting rod b, but I am not sure what the lenth of dimension a should be. I know this is probably simple maths (just pythagoras?) but I need to make sure I get the full travel out of rod c with full 360 degree rotation on the axel.
It would normally be very simple (a = 0.5 x travel of rod c), but it is the fact that rod b is allowed to pivot around the joint to rod c makes it a bit more confusing.
