How Do You Calculate Distance and Direction Using Vector Coordinates?

[geoff18]

Homework Statement

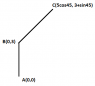
A car travels 3km due North then 5km North East. Use co-ordinate vectors to find the distance and direction from the starting point.

Homework Equations

I understand that co-ordinate vectors meant the column vector, but I don't understand how to convert the above description into vectors. I can calculate the distance by drawing two right angle triangles find the sides and addition it via vector laws and pythag theorm. But I don't think that is what the question wants.

The Attempt at a Solution

I read thru my lecture notes and attempt to google the answers but most of the results just explain using a1=|a|*cos(a) etc

 

[cupid.callin]

Assume the starting position of car as origin. You can plot the coordinates of two points that are being talked about in ques. ( first where car changes direction and second where car is finally.

The vector between any two points A(a,b) and B(c,d) is given as,
Vec(BA) = (c-a)i + (d-b)j

Find two vectors and then add them to get net vector.
The you can find its magnitude

 

[geoff18]

Hi thanks for the prompt reply, rly appreciate it.

so origin would be (0,0)
Second point would be (0,3)
Third Point would be (5/root2, 3+(5/root2))
?

If that is the case, wouldn't the effort to find those co-ordinates already solve the length of the distance?

 

[azizlwl]

Hi thanks for the prompt reply, rly appreciate it.

so origin would be (0,0)
Second point would be (0,3)
Third Point would be (5/root2, 3+(5/root2))
?

If that is the case, wouldn't the effort to find those co-ordinates already solve the length of the distance?

Second point you move up vertically 3 units, so pt.(0,3) correct.
Then you move another 5 units in North east direction, so the pt is (?,?)

The question is how many units are there from (0,0) to (?,?) and direction.

 

[geoff18]

Second point you move up vertically 3 units, so pt.(0,3) correct.
Then you move another 5 units in North east direction, so the pt is (?,?)

The question is how many units are there from (0,0) to (?,?) and direction.

Hi Azizlwl, thanks for the reply.
How would I write the co-ordinates of 5 units moving in north east direction?
Would i need to use pythag's theorm to calculate the co-ordinates?
thanks

 

[HallsofIvy]

Yes, the "northeast" direction is at 45 degrees to both "north" and "east" so the two components are equal. So a^2+ b^2= a^2+ a^2= 5^2.

 

[azizlwl]

Hi Azizlwl, thanks for the reply.
How would I write the co-ordinates of 5 units moving in north east direction?
Would i need to use pythag's theorm to calculate the co-ordinates?
thanks

Yes, maybe with a help of a diagram can make it easier for you find the answers.

 

[geoff18]

so the co-ordinate of the third point will be ((sqrt of 25)/2)),((sqrt of 25)/2))+3))

 

[azizlwl]

Let me rephase again.
You move up 3 units vertically from origin (0,0) to points (0,3) equal to 3 units north.
From point (0,3) you move another 5 units in direction of northeast.
This property of movement is called vector since it has units(magnitude) and direction too.

Northeast means equal north and east.
Direction of northeast means if you move "b" units to north, you have to move another "b" units to the east too.
Now you have moved not only in direction of north but also in direction of east.

Now try to draw the diagram.Later you will be able to draw on you mind without resorting to paper.

 

[geoff18]

so according to this then:
Origin: (0,0)
First point: (0,3)
Second Point: (5,8) [Moved move 5 units right/east AND 5 units up/north]

so the distance should be 5^2+8^2=25+64=89
=sqrt(89) =>9.43(approx)?

The answer states: 7.43 tho?

Did I do something wrong?

 

[azizlwl]

1st pt=(0,0)
2nd. pt=(0,3)
3rd pt =(?,?) NOT (5,8)

Use phytagoras theorem or trig. function find 3rd point.

http://img521.imageshack.us/img521/2084/p1010011wx.jpg

 

[geoff18]

Hi Thanks for the picture azizlwl, so using tri functions, i assume that the point will be:
(5cos(45), ((5*sin(45))+3))

 

[azizlwl]

Hi Thanks for the picture azizlwl, so using tri functions, i assume that the point will be:
(5cos(45), ((5*sin(45))+3))

Correct.

 

[cupid.callin]

Hi Thanks for the picture azizlwl, so using tri functions, i assume that the point will be:
(5cos(45), ((5*sin(45))+3))

​

Hi geoff18 ...
So now you have found all the three points as shown above. Now you can find the Vectors BA and CB as i told you before

The vector between any two points A(a,b) and B(c,d) is given as,
Vec(BA) = (c-a)i + (d-b)j

But what I am not sure is how you are supposed to proceed now ...
There are two (common) ways to proceed now,
I. Find BA, CB and then find BA using vector addition law.
II. Directly find CA using points C and A

Anyone would use II method but as i am unaware of what you are supposed to do, i will and must leave that decision for you :D

EDIT: C will be (3 + 5 sin 45)