How Do You Calculate Minimum and Maximum Velocities in Projectile Motion?

[CherryWine]

PROBLEM REGARDING PROJECTILE MOTION
1.

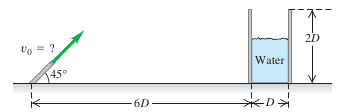
I have to find the implicit equation for minimum and maximum initial velocity needed in order for water to end up in the reservoir. I have tried solving it by firstly expressing flight time from the equation for range of projectile (time in terms of D and Vx). I obtain t=6D/(v0*cosx45) - for minimum velocity. Then I substituted this in the equation of y(t) and obtained the trajectory equation. From that equation y(x), I expressed initial velocity and obtained V0=sqrt((D^2*g)/(2(cosx)^2*deltaY-2(cosx)^2*tanx*D)), and from there I obtained Vmin=2,44*sqrt(D*g) and Vmax=2,65*sqrt(D*g) while the correct answers are Vmin=3*sqrt(D*g) and Vmax=3,13*sqrt(D*g). I couldn't figure what was wrong in my method.

Edit: Please note that in the trajectory equation D means the range (6D and 7D), I did not use just one D for calculation. Also in trigonometric functions x is the angle=45 degrees. DeltaY is 2D.

Homework Equations

D=V0*cosx*t
t=D/(V0*cosx)
deltaY=V0*sinx*t+1/2*gt^2

 

[Fightfish]

Sorry, I can't quite follow your train of thought. Could you could show us the equation of the trajectory, y(x), that you found?
Note that the requirement that the projectile lands in the water sets the following 2 constraints: (1) y(6D) \geq 2D and (2) y(7D) < 2D. Imposing these constraints will lead to two inequalities that will get you the minimum and maximum v_{0} allowed.

 

[CherryWine]

Sorry, I can't quite follow your train of thought. Could you could show us the equation of the trajectory, y(x), that you found?
Note that the requirement that the projectile lands in the water sets the following 2 constraints: (1) y(6D) \geq 2D and (2) y(7D) < 2D. Imposing these constraints will lead to two inequalities that will get you the minimum and maximum v_{0} allowed.

The trajectory equation I obtained is y(x)=v0*sinθ*((6D)/(v0*cosθ))+1/2*g*((6D^2*g)/(2v0^2*(cosθ)^2)). Which then simplifies to y(x)=tanθ*6D+((6D^2*g^2)/(2*v0^2*(costheta)^2)).

 

[Fightfish]

Given that \theta = 45^{o}, you could have made your life a lot easier. What you have is not a trajectory equation - you have already evaluated the y-position at that particular point, but that works too - if your equation was correct. Remember that g acts downwards (and it shouldn't be squared in the expression as well?)

 

[CherryWine]

Sorry, I can't quite follow your train of thought. Could you could show us the equation of the trajectory, y(x), that you found?
Note that the requirement that the projectile lands in the water sets the following 2 constraints: (1) y(6D) \geq 2D and (2) y(7D) < 2D. Imposing these constraints will lead to two inequalities that will get you the minimum and maximum v_{0} allowed.

I don't think that you can use the inequality y(6D)>=2D because that could mean that at x=6D, y can be larger than 2D, and then the possibility of the projectile overshooting the reservoir stays open. I think that using strict equations y(6D)=2D and y(7D)=2D would yield the correct answer.

Given that \theta = 45^{o}, you could have made your life a lot easier. What you have is not a trajectory equation - you have already evaluated the y-position at that particular point, but that works too - if your equation was correct. Remember that g acts downwards (and it shouldn't be squared in the expression as well?)

Sorry for the squared g, but the trajectory equation is not the main thing here, it is the equation for Vo that I obtained from it; Vo=sqrt((D^2*g)/(2(costheta)^2*deltaY-2(costheta)^2*tantheta*D)). Could you please find a problem in that equation? (Notice that g is not squared, it was my mistake in the upper post.)

 

[CWatters]

I don't think that you can use the inequality y(6D)>=2D because that could mean that at x=6D, y can be larger than 2D, and then the possibility of the projectile overshooting the reservoir stays open.

That's where the other inequality come in. You need both... y(6D)>=2D and y(7D)<2D. The first stops undershoot and the second stops overshoot. If both are met the water will go in. I don't think both can be met and the water not go in.

 

[Fightfish]

I don't think that you can use the inequality y(6D)>=2D because that could mean that at x=6D, y can be larger than 2D, and then the possibility of the projectile overshooting the reservoir stays open. I think that using strict equations y(6D)=2D and y(7D)=2D would yield the correct answer.

y(6D) and y(7D) cannot both be the same! The projectile follows a parabolic trajectory. That is why there are two constraints, firstly y(6D)\geq 2D to let the projectile go over the first boundary and the second, y(7D) &lt; 2D to ensure that it does not fly over the second boundary.

Sorry for the squared g, but the trajectory equation is not the main thing here, it is the equation for Vo that I obtained from it; Vo=sqrt((D^2*g)/(2(costheta)^2*deltaY-2(costheta)^2*tantheta*D)). Could you please find a problem in that equation? (Notice that g is not squared, it was my mistake in the upper post.)

Any errors from your trajectory equation carry over directly to your expression for v_{0}...
At first glance, you have a sign problem, and some numerical factors are missing. What I got was (using your notation) v_{0,min}^{2} = \frac{36D^{2}g}{2\cos^{2}\theta \left(6D \tan \theta - \Delta y\right)},
which you can check evaluates to v_{0,min} = 3\sqrt{Dg}.

 

[CherryWine]

You will need to show more of your work in order for us to find the error. Are the velocities in this equation supposed to be y-components of velocity?

That's where the other inequality come in. You need both... y(6D)>=2D and y(7D)<2D. The first stops undershoot and the second stops overshoot. If both are met the water will go in. I don't think both can be met and the water not go in.

y(6D) and y(7D) cannot both be the same! The projectile follows a parabolic trajectory. That is why there are two constraints, firstly y(6D)\geq 2D to let the projectile go over the first boundary and the second, y(7D) &lt; 2D to ensure that it does not fly over the second boundary.

Any errors from your trajectory equation carry over directly to your expression for v_{0}...
At first glance, you have a sign problem, and some numerical factors are missing. What I got was (using your notation) v_{0,min}^{2} = \frac{36D^{2}g}{2\cos^{2}\theta \left(6D \tan \theta - \Delta y\right)},
which you can check evaluates to v_{0,min} = 3\sqrt{Dg}.

Yes, you're right for the inequalities. I didn't think about them simultaneously. Sorry. Also Fightfish you are correct with your answer, just checked it both for Vmin and Vmax. My mistake was numerical. Thank you very much.