How Do You Calculate Tension and Angles in a Two-Mass Equilibrium Problem?

[SeanGillespie]

Homework Statement

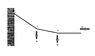
A light inextensible string ABC is fixed at point C. Two particles, each of weight W are attached to the string by A and B. The system is held in equilibrium by a horizontal force of magnitude 2W acting on particle A.

Find (a) the tensions in AB and BC, and (b) the inclinations of AB and BC to the verticle.

2. The attempt at a solution

I understand that the verticle and horizontal components should cancel out as it is in equilibrium.

I have a page scribbled with attempts at finding an answer, however, I am so unsure of myself that I don't wish to stick to any of my techniques as a conclusion. Could someone please hint me through this problem.

 

[kuruman]

Start by showing us the equations that say that the net force on each mass is zero.

 

[SeanGillespie]

Okay, I'll use vector notation.

Particle A:
$$(^{2W}_{ 0}) + (^{ 0}_{-W}) - T_{1} = 0$$

Particle B:
$$(^{2W}_{-W}) + (^{0}_{-W}) - T_{2} = 0$$

I've come to some answers using this, I'm not sure if I'm right or wrong though.

I've arrived at T1 being 2.24W (2 d.p.), and T2 being 2.83W (2 d.p.).

The angles are 63.4 and 45, from the vertical in the negative x-direction.

Have I gone wrong anywhere?

 

[akari]

tension in string AB=root5 W angle of inclanation arctan(2),i think u r right then we can find other things easily

 

[kuruman]

You need to rewrite the equation for particle B. From the equation for particle A you have T1 = (2W, -W). That means a force that acts to the right and down on particle A. Look at the drawing. The rope exerts a force that is to the left and up. The correct T1 is the opposite of what you have, i.e. you should have written +T1 not -T1 in the equation because if you add vectors the sum of all the forces must be zero.

For the equation for particle B note that T1 should be opposite of what it is for particle A. Also, you should put a plus sign in front of T2 for the same reasons as explained above.

 

[SeanGillespie]

Oh yes, sorry.

I skipped part of that calculation in my notes, was an error I made while typing it up on here. Confident that I've got it right now, thank you.