How Do You Calculate the Landing Point of a Projectile Thrown from a Height?

[Darth Frodo]

Homework Statement

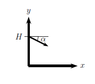
A stone is thrown with a velocity $v_{0}$ at an angle $\alpha$ to the horizontal (see image) from a step of height H. Calculate the x coordinate $x_{1}$ of the point where the stone hits the ground.

Homework Equations

$x(t) = u_{x}t + x_{0}$
$y(t) = u_{y}t + \frac{1}{2}at^{2} + y_{0}$

The Attempt at a Solution

$u_{x} = v_{0}cos(\alpha)$
$u_{y} = -v_{0}sin(\alpha)$

$x_{1} = u_{x}t_{1}$
$x_{1} = v_{0}cos(\alpha)t_{1}$
$y(t) = 0 @ t_{1}$
$0 = -v_{0}sin(\alpha)t_{1} - \frac{g}{2}(t_{1})^2 + H$


Here is where I have a discrepency with the provided (Bare Bones) Solution.

According to the solution; $0 = v_{0}sin(\alpha)t_{1} - \frac{g}{2}(t_{1})^2 + H$

This seems to be missing the "-" in front of the 0 = $v_{0}sin(\alpha)t_{1}$ term.

My question is am I correct?

 

[Tallus Bryne]

You could say that both your result and the solution are correct; they just make different assumptions about how the angle α is determined.

Your result assumes that α is a positive angle which lies between the positive x-axis and the initial velocity vector.

For the given solution to be correct, it is assumed that the angle α must be determined by rotating counter-clockwise from the positive x-axis for positive angles (or clockwise for negative angles).

 

[Gzyousikai]

$$x(t)=v_0\cos\alpha t, y(t)=H+v_0\sin\alpha t-\frac{1}{2}gt^2$$
combine those two parametric equations, we get
$$y=x\tan\alpha-\frac{g\sec^2\alpha}{2v_0^2}x^2+H$$

let y=0 and solve for x