dari09
- 2
- 0
Rotational Inertia Problem--PLEASE HELP!
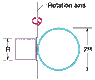
Figure 12-39 shows a rigid structure consisting of a circular hoop, of radius R and mass m, and a square made of four thin bars, each of length R and mass m. The rigid structure rotates at a constant speed about a vertical axis with a period of rotation of 1.0 s. Assuming R = 0.50 m and m = 3.0 kg, calculate the structure's rotational inertia about the axis of rotation
The figure is attached
I of point mass = mr^2
I of hoop = mr^2 or .5mr^2
I of rod = 1/3 mr^2
I tried to add the I of the hoop and two of the rods together (because the other two rods are parallel to the rotating axis) but nothing that I've tried really worked...
Homework Statement
Figure 12-39 shows a rigid structure consisting of a circular hoop, of radius R and mass m, and a square made of four thin bars, each of length R and mass m. The rigid structure rotates at a constant speed about a vertical axis with a period of rotation of 1.0 s. Assuming R = 0.50 m and m = 3.0 kg, calculate the structure's rotational inertia about the axis of rotation
The figure is attached
Homework Equations
I of point mass = mr^2
I of hoop = mr^2 or .5mr^2
I of rod = 1/3 mr^2
The Attempt at a Solution
I tried to add the I of the hoop and two of the rods together (because the other two rods are parallel to the rotating axis) but nothing that I've tried really worked...