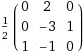How Do You Find the Inverse of a Matrix Using the Adjoint Method?

[karush]

$\textsf{Find the inverse of matrix} $
$$A=\left|
\begin{array}{rrr}
1&0&2\\ 1&0&0 \\ 3&2&0
\end{array}
\right|$$
$\textsf{by method of adjoint matrix }\\$
$\textsf{adj $A = |C_{ij}|^T$}\\$
$\textsf{det $A =4$}\\$
$\textsf{so then}\\$
$A^{-1}=\frac{1}{det A}(adj A)=
\frac{1}{4}(adj A)$
$\textit{ok I don't know how to get (adj A)}$

 

[tkhunny]

It's a little tedious.

Pick each element in the 3x3 matrix, one at a time.

Delete the row and the column and calculate the determinant of the remaining 2x2 matrix.

Replace the selected element with the result.

Do this for each of the nine elements. Some of the results might be 0.

Don't forget the cofactor for each.

Transpose and you are done.

 

[karush]

Pick each element in the 3x3 matrix, one at a time.

Delete the row and the column and calculate the determinant of the remaining 2x2 matrix.

like this?
$A=\left| \begin{array}{rrr} 1&0&2\\ 1&0&0 \\ 3&2&0 \end{array} \right|\\$
$=\begin{bmatrix}0& 0 \\ 2& 0 \\\end{bmatrix}
+0
+2\begin{bmatrix}1& 0 \\ 3& 2 \\\end{bmatrix}
+\begin{bmatrix}0& 2 \\ 2& 0 \\\end{bmatrix}
+0+0
+3\begin{bmatrix}0& 2 \\ 0& 0 \\\end{bmatrix}
+2\begin{bmatrix}1& 2 \\ 1& 0 \\\end{bmatrix}\\$
$=0+0+2(2)-4+0+0+0+2(-2)=-4$

ok W|A says it is 4 ?

 

[tkhunny]

like this?

$A=\left| \begin{array}{rrr} 1&0&2\\ 1&0&0 \\ 3&2&0 \end{array} \right|\\$
$=\begin{bmatrix}0& 0 \\ 2& 0 \\\end{bmatrix}
+0
+2\begin{bmatrix}1& 0 \\ 3& 2 \\\end{bmatrix}
+\begin{bmatrix}0& 2 \\ 2& 0 \\\end{bmatrix}
+0+0
+3\begin{bmatrix}0& 2 \\ 0& 0 \\\end{bmatrix}
+2\begin{bmatrix}1& 2 \\ 1& 0 \\\end{bmatrix}\\$
$=0+0+2(-1)+0+0+0+0+2(-2)=-6$ok W|A says it is 4 ?

No. You calculated them all, but then you added all the pieces. Don't do that. Do one at a time and substitute them into a new matrix - replacing the element you used to produce the smaller matrix. You should get a new 3x3 matrix out of the process.

 

[karush]

No. You calculated them all, but then you added all the pieces. Don't do that. Do one at a time and substitute them into a new matrix - replacing the element you used to produce the smaller matrix. You should get a new 3x3 matrix out of the process.

$$\begin{vmatrix}0& 0& -2 \\ -4& 0& 0\\ 0& -4& 0
\end{vmatrix}$$

not convinced this is correct
but couldn't find error

 

[tkhunny]

$$\begin{vmatrix}0& 0& -2 \\ -4& 0& 0\\ 0& -4& 0
\end{vmatrix}$$

not convinced this is correct
but couldn't find error

Closer, but the Adjunct piece does NOT include the element itself. You still think you're trying to evaluate a determinant. That is not what you are doing. You must find all nine 2x2 matrices and evaluate their determinants. The element is replaced in each case. Don't multiply by it.

 

[karush]

Closer, but the Adjunct piece does NOT include the element itself. You still think you're trying to evaluate a determinant. That is not what you are doing. You must find all nine 2x2 matrices and evaluate their determinants. The element is replaced in each case. Don't multiply by it.

$=\begin{bmatrix}0& 0 \\ 2& 0 \\\end{bmatrix}
+0
+\begin{bmatrix}1& 0 \\ 3& 2 \\\end{bmatrix}
+\begin{bmatrix}0& 2 \\ 2& 0 \\\end{bmatrix}
+0+0
+\begin{bmatrix}0& 2 \\ 0& 0 \\\end{bmatrix}
+\begin{bmatrix}1& 2 \\ 1& 0 \\\end{bmatrix}+0$$\begin{bmatrix}0& 0 &-2 \\ 4& 0 &0 \\ -2& 2& 0 \end{bmatrix}$

W|A gave this as inverse?

View attachment 7985

 

[tkhunny]

$=\begin{bmatrix}0& 0 \\ 2& 0 \\\end{bmatrix}
+0
+\begin{bmatrix}1& 0 \\ 3& 2 \\\end{bmatrix}
+\begin{bmatrix}0& 2 \\ 2& 0 \\\end{bmatrix}
+0+0
+\begin{bmatrix}0& 2 \\ 0& 0 \\\end{bmatrix}
+\begin{bmatrix}1& 2 \\ 1& 0 \\\end{bmatrix}+0$$\begin{bmatrix}0& 0 &-2 \\ 4& 0 &0 \\ -2& 2& 0 \end{bmatrix}$

W|A gave this as inverse?

This is the Adjunct Matrix:

$\begin{bmatrix}0& 0 &2 \\ -4& -6 &2 \\ 0& -2& 0 \end{bmatrix}$

Please reproduce the results.

After applying the cofactors

$\begin{bmatrix}0& 0 &2 \\ 4& -6 &-2 \\ 0& 2& 0 \end{bmatrix}$

Please reproduce the results.

Transpose and you should be done.

 

[karush]

This is the Adjunct Matrix:

$\begin{bmatrix}0& 0 &2 \\ -4& -6 &2 \\ 0& -2& 0 \end{bmatrix}$

Please reproduce the results.

Transpose and you should be done.

Ok I don't see how you got the Adjunct Matrix

what do you mean "reproduce the results"

 

[tkhunny]

This is the Adjunct Matrix:

$\begin{bmatrix}\begin{vmatrix}0& 0 \\ 2& 0 \end{vmatrix}& \begin{vmatrix}1& 0 \\ 3& 0 \end{vmatrix} &\begin{vmatrix}1& 0 \\ 3& 2 \end{vmatrix} \\ \begin{vmatrix}0& 2 \\ 2& 0 \end{vmatrix}& \begin{vmatrix}1& 2 \\ 3& 0 \end{vmatrix} &\begin{vmatrix}1& 0 \\ 3& 2 \end{vmatrix} \\ \begin{vmatrix}0& 2 \\ 0& 0 \end{vmatrix}& \begin{vmatrix}1& 2 \\ 1& 0 \end{vmatrix}& \begin{vmatrix}1& 0 \\ 1& 0 \end{vmatrix} \end{bmatrix}$

Don't ever make me do that again. :-)

Every element is replaced by the determinant of the smaller matrix created be deleting its row and column. The original element is gone. We're creating a new animal.

Supply the cofactors.
Transpose.
You're done.

 

[karush]

I presume this...
$\text{3. } A^{-1}
=\displaystyle\frac{1}{det A}(adj A)
=\frac{1}{4}
\begin{bmatrix}0& 0 &2 \\ -4& -6 &2 \\ 0& -2& 0 \end{bmatrix}$

 

[tkhunny]

Seems there should be a Transpose in there.

Please check your results. Multiply by the original matrix. What should be the result?

 

[karush]

thusly...

$\text{3. } A^{-1}
=\displaystyle\frac{1}{det A}(adj A)
=\frac{1}{4}
\begin{bmatrix}
0& 0 &2 \\ -4& -6 &2 \\ 0& -2& 0
\end{bmatrix}^T
=\frac{1}{4}
\begin{bmatrix}
0& -4 &0\\ 0& -6 &-2 \\ 2& 2& 0
\end{bmatrix}$
$= \begin{bmatrix}
0& -1 &0\\ 0& -3/2 &-1/2 \\ 1/2& 1/2& 0
\end{bmatrix}$

 

[tkhunny]

Did you check it?

 

[karush]

I know there are errors but couldn't find them

 

[tkhunny]

I know there are errors but couldn't find them

Keep looking.

Be more careful and systematic.

You'll learn more. Plus, the process will annoy you a little and you'll be even more careful on the next problem.