John Greger
- 34
- 1
Homework Statement
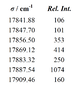
The Ca spectrum below, recorded using a Fourier Transform Spectrometer (FTS), shows the resolved ##3d4s ^3D - 3d4p ^3D## multiplet. The wavenumbers and their relative intensities are given in the table. Identify all the lines and determine the fine structure constants in the two triplets (both are positive).
Homework Equations
[/B]
$$I=F_{max} - J (1)$$
Landé interval rule: ##\frac{F_{max}}{F_{max-1}} = ##energy ratio between the F numbers(2)
$$ E_{hfs} = A/2 * [F(F+1) - J(J+1)-I(I+1)] (3)$$
The Attempt at a Solution
[/B]
I can determine the quantum numbers F,,J,I. But how do I know what rel. int. correspond to what transition?
And once I have the transitions. How do I use eq.(3) to solve for A?
Very grateful for any reply!