Precursor
- 219
- 0
Homework Statement
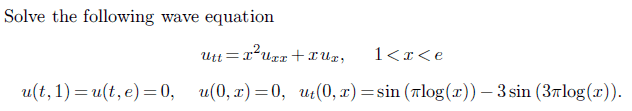 The attempt at a solution
The attempt at a solution
I'm using the method of separation of variables by first defining the solution as u(x,t) =X(x)T(t)
Putting this back into the PDE I get: T''X = x^{2}X''T + xX'T
which is simplified to \frac{T''}{T} = \frac{x^{2}X'' + xX'}{X} = -\lambda^{2}
The spatial problem is then: x^{2}X'' + xX' = -X\lambda^{2}
Is this correct so far? How do I continue?
I'm using the method of separation of variables by first defining the solution as u(x,t) =X(x)T(t)
Putting this back into the PDE I get: T''X = x^{2}X''T + xX'T
which is simplified to \frac{T''}{T} = \frac{x^{2}X'' + xX'}{X} = -\lambda^{2}
The spatial problem is then: x^{2}X'' + xX' = -X\lambda^{2}
Is this correct so far? How do I continue?