Touchme
- 41
- 0
Homework Statement
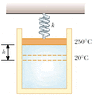
An expandable cylinder has its top connected to a spring with force constant 2.00 103 N/m. (See Fig. P10.58.) The cylinder is filled with 6.00 L of gas with the spring relaxed at a pressure of 1.00 atm and a temperature of 20.0°C.
I searched for a similar question however I didnt understand it. Maybe it was the calculation error. Someone help me...
Homework Equations
PV = nRT
[PV/T]i = [PV/T]f
Volume of cylinder = Ah
The Attempt at a Solution
First I convert my units. Initial state: 101325 Pa, 293 K, and 0.006 m^3
I determined the constant by using the gas law PV/T. (101325)(0.006)/293 = 2.0749 [(Nm^2)/K].
After the temperature is increased to 503 K (273+230), the piston rises and the volume changes. The new volume is 0.006 + Ah = 0.006 + 0.01h. The pressure is equal to P = F/A. F is the force constant times dispalcement (h), which is 2000 N/m. P = 2000/0.01 = 200000h N/m^2.
Putting everything together we get
2.0749 = (200000h)(0.006+0.01h)/503
The answer h = 0.482 m or 48.2 cm is incorrect. Any suggestion or corrections. Thank you.
Attachments
Last edited: