KingBigness
- 94
- 0
Homework Statement
See attached photo
The Attempt at a Solution
So I have no idea if I have even started this problem correctly so any help would be nice.
My working is set out in one of the pictures.
Any help would be appreciated I really am not quite sure what to do. Can't figure out where the x^2-y^2 comes from.
Thank you!
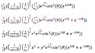
 , but if you replace r2sin2θcos2φ by r2sin2θ(cos2φ - sin2φ), that looks like x2 - y2
, but if you replace r2sin2θcos2φ by r2sin2θ(cos2φ - sin2φ), that looks like x2 - y2 