How do you use a Rotation Matrix in 2-D?

[Saladsamurai]

I am having some trouble deciphering what the input and output of a 2D Rotation Matrix actually represent.

All example online have the vectors oriented at the origin. I know you can move them anywhere so long as you maintain their length and orientation, but here is my question:

Let's say I have a vector that is not located at the origin. Call its initial point (x₀, y₀) and its terminal point (x₁, y₁)

Now let's say that it has rotated through the positive angle of Phi. It's initial point is clearly still (x₀, y₀) and its new terminal point is (x₂, y₂).

Using only (x₀, y₀) and angle Phi, how can I find the coordinate (x₀, y₀) ?

I know that the Rotation Vector is defined as:

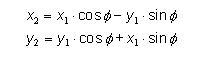
My issue is that since they chose the origin, x₁ and y₁ in their example could be either the coordinates OR the components.

So, for the general 2D case: Do I plug in the coordiantes or components? And are the results the coordinates or components?

I am under the impression that it is the latter in both cases. And so in order to obtain the actual coordinates of my new vectors endpoint, I must add the resulting components to the initial coordinate (x₀, y₀)

Does that sound right?

 

[CompuChip]

Well, you can move it to the origin, rotate it, and move it back.

So if v = (x₀, y₀) and w = (x₁, y₁), then: a) calculate w - v; b) apply the rotation matrix to obtain a new vector z; c) calculate z + v.

 

[kuruman]

If the tail of the vector r that you want to rotate is not at the origin, then find the position vector R of the tail with respect to the arbitrary origin and use the matrix to rotate the sum R+r. The result will be the coordinates of the tip of rotated vector r. To find the coordinates of the rotated tail, use the matrix once more on R.

 

[Saladsamurai]

I just wrote a code to test a few cases of what I said in the OP, and this is the formula I came up with. I think it is consistent with what you guys are saying:

r_x = x1 - x0
r_y = y1 - y0

x2 = x0 + (r_x * Cos(theta) - r_y * Sin(theta))
y2 = y0 + (r_y * Cos(theta) + r_x * Sin(theta))