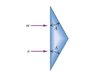
How Does a Prism Affect the Angle Between Two Emerging Light Rays?

[Twigs]

A prism shown i has a refractive index of n, and the angles A are theta. Two light rays m and n are parallel as they enter the prism.

What is the angle between them after they emerge?(In radians)

 

[dextercioby]

What did you do/try to do...?

Daniel.

 

[Twigs]

I assume you use n_1*sin(theta)=n_2*sin(theta_2).

And since its 90 degrees, it would just be equal to 1, so I get 1=n_2*sin(theta_2) but I am afraid that I am assuming too much. Then you do it again for the light going out of the prism.

 

[dextercioby]

Because of the normal incidence,the rays enter the prism nondeviated...You must apply Snell'-Descartes law for the outgoing...

Daniel.

 

[Twigs]

I get angle(rads.)= arcsin(n*sin(theta))

 

[Twigs]

no, that's answer is wrong, any help?

 

[dextercioby]

I'm really sorry,i cannot give you any more details,because it's basically a geometry problem.The incident angle is "\theta" for both rays...Compute the reflection angle,which is indeed "\arcsin (n\sin\theta)" and then use the symmetry of the problem and basic geometry knowledge to solve it...

Daniel.

 

[Twigs]

2*arcsin(n*sin(theta))+pi/2
heres my new answer.

 

[dextercioby]

I'm getting angle=2[\arcsin (n\sin\theta)-\theta]

Daniel.