How Does Ampere's Law Treat External Currents in Magnetic Field Calculations?

[cupid.callin]

In ampere circuital law, ∫B.dl = μ_o i_net
i includes current "only passing through the loop "

also B is the net mag field at any point "all to any current anywhere"

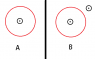
now look at the pic.

In A, it is very easy to find field using ampere law ... its μi/2πr

Also if in B is you apply the law, B is again μi/2πr ... how is this possible
its like the external current doesn't make any difference!

Plz explain me this !

 

[Clever-Name]

Ampere's law relies on what you define to be your curve of integration. Ampere's law states that the closed-loop integral Bdl over a given curve is proportional to the net current ENCLOSED by said loop.

In A you only have 1 wire enclosed by your curve of integration (red circle). In B, yes there are 2 wires, but only one is enclosed by your curve of integration, thus the same answer as in A.

 

[cupid.callin]

Ampere's law relies on what you define to be your curve of integration. Ampere's law states that the closed-loop integral Bdl over a given curve is proportional to the net current ENCLOSED by said loop.

In A you only have 1 wire enclosed by your curve of integration (red circle). In B, yes there are 2 wires, but only one is enclosed by your curve of integration, thus the same answer as in A.

So you are saying that i studied it wrong that in Bdl B is not due to all the currents existing in space?

 

[Fightfish]

So you are saying that i studied it wrong that in Bdl B is not due to all the currents existing in space?

No, no, you are correct. B is due to the combined effect from all the currents.

Also if in B is you apply the law, B is again μi/2πr ... how is this possible
its like the external current doesn't make any difference!

The integral \oint \vec{B} \cdot \vec{dl} gives the same result, but you cannot pull |\vec{B}| out like that because it is not constant in this case, unlike in the first!

 

[cupid.callin]

Oh yes! you are right!

How can i ignore that thing !

Dumb of me !

Thanks a lot Fightfish !