How Does Bullet Impact Affect Spring Compression in a Frictionless System?

[stunner5000pt]

have a look at the diagram
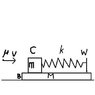
A physical system consists of wood block B and mass M. B is at rest on frictionless horizontal table. A small vertical wall W is place near one of the ends of B. The wall is fastened to B.A spring with spring constant k is attached to the wall and is connected tp a block C. of mass m.

No friction between C and B. A bullet of mass mu \mu is shot is shot into block C. The velocity v is parallel to the table. The spring does not bend.
Assume that the bullet is stopped in such a short time taht t is negligible. The spring mass and the wall mas are neglected

a) find the maximum compression d of the spring, in terms of v, k, M , m and \mu

bullet goes into the block inelastically so
\mu v = (\mu + m) v_{f}
and v_{f} = \frac{\mu v}{\mu + m}

this vf (kinetic energy) is converted to spring energy
\frac{1}{2} (\mu + m) (\frac{\mu v}{\mu + m})^2 = \frac{1}{2} kx^2
and thus x = \mu v \sqrt{\frac{1}{k(\mu + m)}}
this is assuming that x = \Delta L + D
and D is converted to the enrgy that makes this thing go forward

so \frac{1}{2} k D^2 = \frac{1}{2} ( \mu + m + M ) v_{f}^2
D = v_{f} \sqrt{\frac{\mu + m + M}{k}}
now here's the dilemma, what is v?? i cannot find D without using some unknown velocity
how would i use the conservation of momentum here?

 

[Gokul43201]

...

a) find the maximum compression d of the spring, in terms of v, k, M , m and \mu

When the spring is at maximum compression, what is the relative velocity between m and M ?

 

[stunner5000pt]

When the spring is at maximum compression, what is the relative velocity between m and M ?

would it be zero??
I'm no quite sure why, though.

 

[learningphysics]

would it be zero??
I'm no quite sure why, though.

Yes, it is zero. Imagine you're sitting on the big mass M watching the spring compress. Initially it is moving to the right (positive relative velocity). Then it gets to maximum compression. Then it moves to the left(negative relative velocity). So at maximum compression we are right at the point where the relative velocity goes from positive to negative. In other words it is at 0 relative velocity at maximum compression.

 

[stunner5000pt]

if the relative velocities are zero then are their momenta the same but in opposite directions??

so (m+ \mu) v = Mv ??

 

[StatusX]

Their velocities are the same. The total momentum has to be equal to the initial momentum of the bullet, from which you can calculate this velocity.

 

[stunner5000pt]

so if the total momenta of the two masses (mass+bullet and slab) is equal to the initial momentum of the bullet

\mu v = (\mu + m) v_{f} + Mv_{f}
and v_{f} = \frac{\mu v}{\mu + m + M} ??

is this what you meant statusx?

 

[learningphysics]

so if the total momenta of the two masses (mass+bullet and slab) is equal to the initial momentum of the bullet

\mu v = (\mu + m) v_{f} + Mv_{f}
and v_{f} = \frac{\mu v}{\mu + m + M} ??

is this what you meant statusx?

Yes. This is right. Now you can use conservation of energy to solve for the compression.

 

[stunner5000pt]

ok so then this leads me to
D = \frac{\mu v}{\mu + m + M} \sqrt{\frac{\mu + m + M}{k}} = \mu v \sqrt{\frac{1}{k(\mu + m + M)}}
sub back into that expression for x = L + D
L = x - D = \frac{\mu v}{\sqrt{k}} (\frac{1}{\sqrt{\mu + m}} - \frac{1}{\sqrt{\mu + m + M}})

L = \frac{\mu v}{\sqrt{k}} (\frac{M}{\sqrt{(\mu+m)(\mu + m + M)}(\sqrt{\mu + m + M} + \sqrt{\mu + M})}
whioch doesn't lead to the answer which is supposed to be
L = \mu v \sqrt{\frac{M}{k(\mu + m + M)(\mu + m}}
... what did i do wrong??

 

[StatusX]

You need to equate the kinetic energy right after the collision (because energy is lost to heat in the collision) with the total energy at the max compression point.

 

[stunner5000pt]

kinetic energy just after the collision is K_{after collision} = \frac{1}{2} \frac{(\mu v)^2}{\mu + m}

the spring compression energy is S = \frac{1}{2} k D^2

right?

the bullet+box and slab system are moving with velocity Vf
K_{sys} = \frac{1}{2} (\mu + m + M) (\frac{\mu v}{\mu + m + M})^2 = \frac{1}{2} \frac{\mu^2 v^2}{\mu + m + M}

K_{after collision} = S + K_{system} yields the answer i need, thank you very much!