How Does Charge Distribution Affect Gaussian Surface Flux?

[tomrja]

Homework Statement

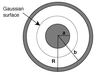
A metal sphere of radius a is surrounded by a metal shell of inner radius b and outer radius R, as shown in the diagram below. The flux through a spherical Gaussian surface located between a and b is 1.20Q/εo and the flux through a spherical Gaussian surface just outside R is 0.80Q/εo.

a) What is the total charge on the inner sphere? (Express your answer as a multiple of Q. For example, if the total charge is 0.2Q, then input 0.2).

b) What is the surface charge density of the inner sphere? (Express your answer as a multiple of Q/a2.)

c) What is the total charge on the inner surface of the outer sphere? (Express your answer as a multiple of Q.)

d) What is the surface charge density of the outer surface of the outer sphere? (Express your answer as a multiple of Q/R2.)

Homework Equations

\phi= integral(E dot dA)= Qenclosed/epsilon not

The Attempt at a Solution

I tried to find the charge enclosed but no charges were given. I don't know how the flux between a and b and the flux through a spherical Gaussian surface come into play. Thanks for your help!

 

[SammyS]

What does Gauss's Law tell you?

 

[AlexChandler]

Flux is equal to the charge enclosed within the surface divided by a constant. This is Gauss' Law.
So for the surface between a and b, say the radius of the surface is r,

\phi_E = 1.20Q/ \epsilon_0 = q_{enc}^r / \epsilon_0

where q_{enc}^r is the charge enclosed within the radius r

Then you also have for the gaussian surface outside R:

\phi_E = 0.80Q/ \epsilon_0 = q_{enc}^R / \epsilon_0

These relations should help