Saad
- 18
- 0
Incline forces question..really hard
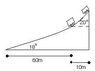
Just recently NASCAR has increased the incline of their race track curves to 18 degrees at the bottom of the curve and 20 degrees at the top. The bottom part of the track (18 degrees incline) has a radius of 60m, where as the top part of the track (20 degrees incline) has a radius of 70m.
a) Using the apropriate free body diagram, derive the equation for the maximum safe speed to negotiate a frictionless banked curve.
b) Neglecting friction, what percentage increase in velocity can be achieved at the top part of the curve (compared with the traditional 18 degrees bank)?
c) If the radius of curvature of the curve for the bottom is 60m and 70m at the top, would the car at the top be able to pass a car on the bottom if they went around half of a circular path at their maximum speeds?
Just recently NASCAR has increased the incline of their race track curves to 18 degrees at the bottom of the curve and 20 degrees at the top. The bottom part of the track (18 degrees incline) has a radius of 60m, where as the top part of the track (20 degrees incline) has a radius of 70m.
a) Using the apropriate free body diagram, derive the equation for the maximum safe speed to negotiate a frictionless banked curve.
b) Neglecting friction, what percentage increase in velocity can be achieved at the top part of the curve (compared with the traditional 18 degrees bank)?
c) If the radius of curvature of the curve for the bottom is 60m and 70m at the top, would the car at the top be able to pass a car on the bottom if they went around half of a circular path at their maximum speeds?
Attachments
Last edited: