How Does Light Emerge from a Prism Using Snell's Law?

In summary, Snell's Law is a fundamental principle in optics that describes how light is refracted when traveling through different mediums. It is particularly relevant in the case of prisms, where it explains the dispersion of colors as light enters and exits the prism. The angle of refraction in a prism can be calculated using the formula n1*sinθ1 = n2*sinθ2, and is affected by the refractive index and shape of the prism. Snell's Law can be applied to all types of prisms, with the angle of deviation varying depending on the prism's material and shape. In real-world applications, Snell's Law and prisms are used in the design of eyeglasses, camera lenses, spectroscopy,
  • #1
PeachBanana
191
0

Homework Statement



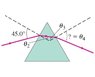
Light is incident on an equilateral glass prism at a 45.0 °angle to one face. Calculate the angle at which light emerges from the opposite face. Assume that n = 1.49.
θ4 = ?

Homework Equations



n1 * sin θ1 = n2 * sin θ2

The Attempt at a Solution



n1 = 1.00 (air)
n2 = 1.49
sin 45° = 0.707

n1 * sinθ1 / 1.49 = sin θ2

sin θ 2 = 0.474
θ2 = 28.33°

I'm having trouble finding θ3.

n2 = 1.49
θ2 = 28.33°
n3 = 1.49
θ3 = ??
 

Attachments

  • GlassPrism.jpg
    GlassPrism.jpg
    6.5 KB · Views: 1,394
Last edited:
Physics news on Phys.org
  • #2
I suggest that you draw a diagram. Then knowing the angle you just found, you can calculate the angle at which the light is incident from glass to air at the second face of the prism.
Then use the same method as before.
 

FAQ: How Does Light Emerge from a Prism Using Snell's Law?

1. What is Snell's Law and how is it related to prisms?

Snell's Law is a fundamental principle in optics that describes the relationship between the angle of incidence and the angle of refraction when light travels through different mediums. In the case of prisms, Snell's Law explains how light is refracted as it enters and exits the prism, resulting in the dispersion of colors.

2. How do you calculate the angle of refraction using Snell's Law with a prism?

The angle of refraction can be calculated using the formula: n1*sinθ1 = n2*sinθ2, where n1 and n2 are the refractive indices of the two mediums and θ1 and θ2 are the angles of incidence and refraction, respectively. In the case of prisms, the angle of refraction can be determined by measuring the angle of incidence and using the known refractive index of the prism material.

3. What is the relationship between the angle of deviation and the angle of incidence in a prism?

The angle of deviation is the difference between the angle of incidence and the angle of refraction in a prism. This means that as the angle of incidence increases, the angle of deviation also increases. However, the angle of deviation can also be affected by the refractive index of the prism material and the shape of the prism.

4. Can Snell's Law be used with all types of prisms?

Yes, Snell's Law can be used with all types of prisms as long as the material has a refractive index and the shape of the prism allows for the refraction of light. However, the angle of deviation may vary depending on the shape and material of the prism.

5. What are some real-world applications of using Snell's Law with prisms?

Snell's Law and prisms have many practical applications, such as in the design of eyeglasses, camera lenses, and other optical instruments. Prisms are also commonly used in spectroscopy to analyze the composition of light. Additionally, prisms are used in many scientific experiments and demonstrations to demonstrate the dispersion of light and properties of refraction.

Similar threads

Red and Violet Light through a Prism (Snell's Law)
Replies
6
Views
9K
Applying Snell's Law Inside & Outside a Prism
Replies
2
Views
2K
Deriving Equation Relating Angle of Incidence to the Angle of Refracti
Replies
6
Views
2K
Monochromatic Light and a Prism
Replies
15
Views
9K
How Does Light Refract Through a Prism with Different Angles?
Replies
1
Views
2K
Snell's Law Application Homework Problem
Replies
1
Views
4K
Angular spread of light rays passing through a prism
Replies
6
Views
4K
What Angle Does Light Emerge from a Prism?
Replies
4
Views
2K
How Do You Calculate the Index of Refraction in a Prism?
Replies
4
Views
14K
Calculate Incident Angle for Snell Optics Problem | n1=1, n2=1.5
Replies
3
Views
9K

Hot Threads

Recent Insights

Back
Top