How Does the Angle Theta Affect the Velocity Calculation in String Problems?

[vcsharp2003]

Homework Statement

Two similar fixed pulleys with the arrangement as shown in diagram have the vertical string ends moving down at U m/s. If the string over pulley is inelastic then what would be the speed of mass M at any given instant of time?

Relevant Equations

Resolve velocity U in vertical and horizontal components

The way I tried to solve it is by using following reasoning.

The inclined part of the string will each have a speed of U m/s. So the point P just above mass M where the inclined strings meet is being moved up by each inclined string at $U \cos {\theta}$. Therefore, the speed of the point P is $2U \cos {\theta}$. This is not the correct answer, which is given as $\dfrac {U} {\cos {\theta}}$. Why is my reasoning not correct?

My attempt is as in screenshot below.

 

[phinds]

Nearly as I can tell, your math approach is correct (U cos theta) but part of your reasoning is flawed. The "2" is a misunderstanding on your part. The system is mirror symmetrical about a vertical line through P and since you are give U, it is irrelevant that it's happening on both sides. You're getting distracted by an unconscious calculation of FORCE, which has nothing to do with the actual question.

So ... I get U cos theta. Who says it is otherwise?

 

[vcsharp2003]

Nearly as I can tell, your math approach is correct (U cos theta) but part of your reasoning is flawed. The "2" is a misunderstanding on your part. The system is mirror symmetrical about a vertical line through P and since you are give U, it is irrelevant that it's happening on both sides. You're getting distracted by an unconscious calculation of FORCE, which has nothing to do with the actual question.

So ... I get U cos theta. Who says it is otherwise?

That is the answer given.

I thought point P would move with a resultant velocity of the two velocities from incline strings acting at point P.

 

[phinds]

That is the answer given.

Yes, I got that. By WHOM? The book? Well, books sometimes give the wrong answer. If it were your prof on a blackboard it could be that he just made a trivial mistake.

I thought point P would move with a resultant velocity of the two velocities from incline strings acting at point P.

Yes, I understand that and as I explained you are wrong and you are wrong for the reason that I gave.

 

[PeroK]

That is the answer given.

I thought point P would move with a resultant velocity of the two velocities from incline strings acting at point P.

You need to draw two diagrams. One at an initial state and another when each of the strings has moved a distance $u\Delta t$, where $\Delta t$ is small. How much higher is the mass?

 

[vcsharp2003]

Yes, I got that. By WHOM? The book? Well, books sometimes give the wrong answer. If it were your prof on a blackboard it could be that he just made a trivial mistake.Yes, I understand that and as I explained you are wrong and you are wrong for the reason that I gave.

It's the answer in textbook.

One of my friends said that $v \cos {\theta} = U$ and then $v = \dfrac {U} {\cos {\theta}}$ but it doesn't make sense to me.

 

[phinds]

One of my friends said that $v \cos {\theta} = U$ and then $v = \dfrac {U} {\cos {\theta}}$ but it doesn't make sense to me.

Me either. Perhaps he was standing on his head when he did it and got confused about what "cos Θ" means.

 

[vcsharp2003]

You need to draw two diagrams. One at an initial state and another when each of the strings has moved a distance $u\Delta t$, where $\Delta t$ is small. How much higher is the mass?

This is what I get by applying the cosine rule.

 

[vcsharp2003]

You need to draw two diagrams. One at an initial state and another when each of the strings has moved a distance $u\Delta t$, where $\Delta t$ is small. How much higher is the mass?

Another approach I tried is by using derivatives as shown in screenshot below. The length c is constant since it doesn't charge with time.

If I use the $\triangle {t}$ approach, I don't end up with an appropriate equation.

 

[haruspex]

One of my friends said that $v \cos {\theta} = U$ and then $v = \dfrac {U} {\cos {\theta}}$ but it doesn't make sense to me.

Your friend is correct. The instantaneous rate at which the joint just above M approaches a pulley is $v\cos(\theta)$. This must equal the rate at which the string passes over the pulley.
It helps to consider an extreme case. As $\theta$ approaches $\pi/2$, what happens to the relative values of u and v?

 

[vcsharp2003]

Your friend is correct. The instantaneous rate at which the joint just above M approaches a pulley is $v\cos(\theta)$. This must equal the rate at which the string passes over the pulley.

Is this because we are breaking velocity of P into two perpendicular components, one of which is along the inclined string?

If I use derivatives to solve this question as in post#9 then also I get the same answer that you have mentioned.

 

[haruspex]

Is this because we are breaking velocity of P into two perpendicular components, one of which is along the inclined string?

It's not a result of analysing it in any particular way. It is true via any valid analysis. But certainly analysing that way helps to make it evident.

 

[Herman Trivilino]

I thought point P would move with a resultant velocity of the two velocities from incline strings acting at point P.

Note that you can have two forces acting on an object, with the net force being the vector sum of those two forces. The same scheme cannot be applied to velocity. You can't have an object moving with two different velocities.

Certainly you can have two components of any vector (be it a velocity vector or a force vector) where the vector sum of the two components equals the original vector.

 

[vcsharp2003]

Note that you can have two forces acting on an object, with the net force being the vector sum of those two forces. The same scheme cannot be applied to velocity. You can't have an object moving with two different velocities.

That's a brilliant point and one that I wasn't aware of.

However in problems of a boat moving across a river that has a current, I've successfully used the concept of two velocities being imparted to the boat. My reasoning has been that the boat can give itself a certain velocity due to its engine and at the same time the river current tries to impart it a velocity. The final velocity will be the vector sum of these velocities being imparted to the boat. Is there a fallacy in my reasoning?

 

[haruspex]

Note that you can have two forces acting on an object, with the net force being the vector sum of those two forces. The same scheme cannot be applied to velocity. You can't have an object moving with two different velocities.

Hmmm...
If forces $\vec F_1, \vec F_2$ act on mass m then the resulting acceleration is $\frac 1m\vec F_1+\frac 1m\vec F_2$, and over time the velocity is $\frac 1m\int\vec F_1.dt+\frac 1m\int\vec F_2.dt$. We can think of this as the sum of the two velocities resulting from the two forces.
It's unusual, I agree, but it is valid.

Wrt relative velocities, as @vcsharp2003 mentions above, they can also be derived from force addition. We may have an actual force applied and be working in an accelerating reference frame leading to a virtual force. Adding these forces is exactly equivalent to adding the velocity of the frame and the relative velocity produced by the applied force.

 

[Lnewqban]

Why is my reasoning not correct?

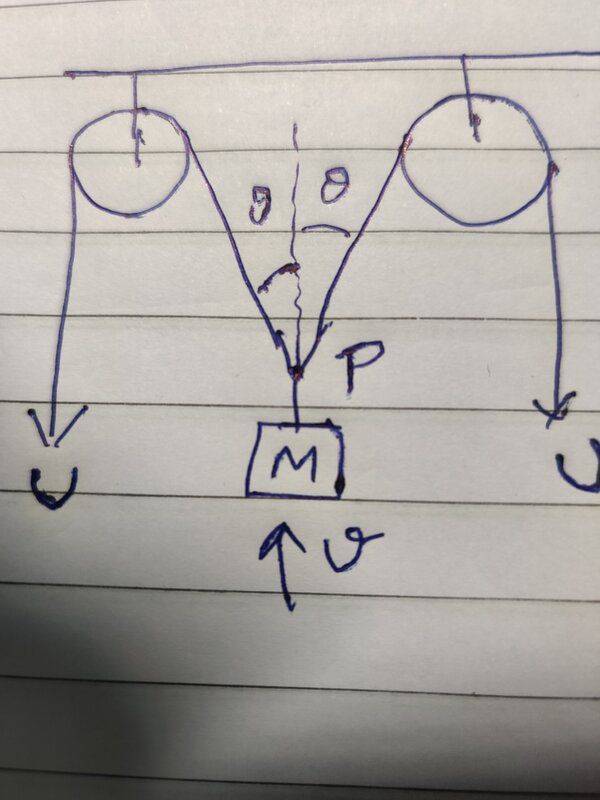
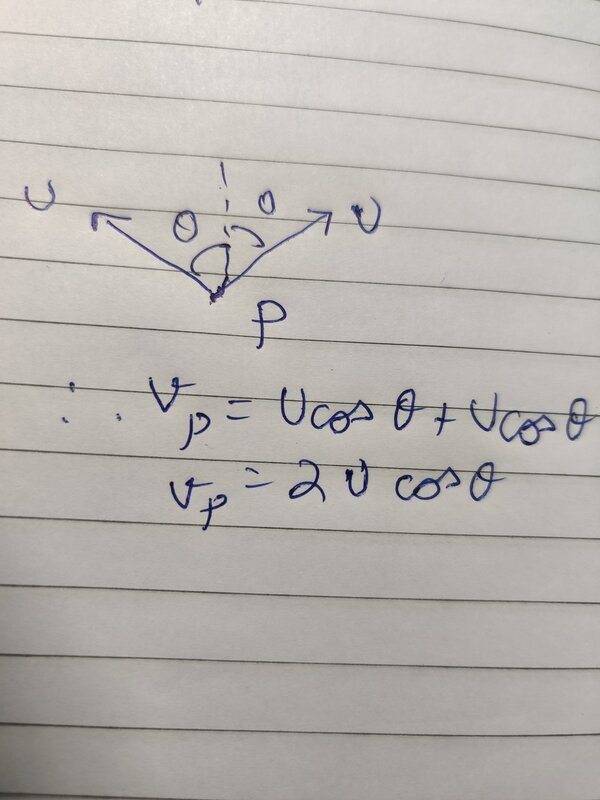
My attempt is as in screenshot below.

View attachment 281416

It is important that you understand the reason that makes your reasoning not correct.
Point P can't have any of those U velocity vectors.
The points of the strings next to point P don't have velocity U, they will move more or less as P will.
Point P is limited to move vertically only, because the symmetrical nature of the forces and geometry in this case.
The only velocity vector for point P, respect to frame of reference formed by the axis of the pulleys, has value V and its direction is aligned with the vertical.

We could also simplify the problem to analyze the left side only if we can imagine that the point P is forced to slide within a vertical slot that is fixed respect to the axes of the pulleys, and that the radii of the pulleys is very small.

Imagine that the section of string that runs between the left small pulley and point P has 10 sections of length=1 unit each.
Section #10 is the closest to the pulley and section #1 is the closest to point P.

The velocity vector for section #10 has value U and its direction is aligned with the string.
The velocity vector for section #1 has value V and its direction is aligned with the vertical (the slot that guides P).
That means that while section #9 takes the place of section #10, the string shortens and rotates counter-clockwise some simultaneously.
That rotation responds to the different directions of vectors U (for #9) and V (for #1).

After resolving the problem graphically, the following is my understanding regarding the relation between U and V based on the geometry of the problem, in case it can help you:

1) As the left side string gets shorter at a constant rate because U of the vertical string beyond the left pulley, the distance that P moves up within our vertical slot for each of our ten sections of the string is bigger than the length of each section.

2) The vertical distances increase respect to each section as P moves up.

3) As the vertical distance that P moves is greater than the length that the string shortens in the same time, the average value of V is greater than U.

4) As the individual values of V increase as the height reached by P increases, there is a positive vertical acceleration until the moment the string reaches a horizontal position.

5) The angular velocity of the string increases as the height reached by P increases; therefore, the string has a positive angular acceleration.

6) Both accelerations rapidly increase as the string gets closer to the horizontal position.

Considering
H the hypotenuse of the triangles successively formed,
h the distances between point P and the top of the slot (90° angle of the triangles) and
k the horizontal distance between the left pulley and the slot, which is constant and has the length towards which H tends,
we have:

$h=\sqrt {H^2-k^2}$

Considering k=4 units:
For t=0, H=10, then h=9.16 units
For t=1, H=9, then h=8.06 units and Δh=1.10
For t=2, H=8, then h=6.92 units and Δh=1.13
For t=3, H=7, then h=5.74 units and Δh=1.17
For t=4, H=6, then h=4.47 units and Δh=1.27
For t=5, H=5, then h=3.00 units and Δh=1.47
For t=6, H=4 (string is horizontal), then h=0 units and Δh=3.00 (note the sudden increase).

 

[vcsharp2003]

Point P is limited to move vertically only, because the symmetrical nature of the forces and geometry in this case.

I guess if point P was not constrained by the strings in its motion but free to move like a boat in a flowing river (as mentioned in post#14), then we could have applied the concept of multiple velocities trying to guide it and added these multiple velocity vectors to get resultant velocity of point P. Is that correct?

 

[Herman Trivilino]

I guess if point P was not constrained by the strings in its motion but free to move like a boat in a flowing river (as mentioned in post#14), then we could have applied the concept of multiple velocities trying to guide it and added these multiple velocity vectors to get resultant velocity of point P. Is that correct?

No. See below.

However in problems of a boat moving across a river that has a current, I've successfully used the concept of two velocities being imparted to the boat. My reasoning has been that the boat can give itself a certain velocity due to its engine and at the same time the river current tries to impart it a velocity. The final velocity will be the vector sum of these velocities being imparted to the boat. Is there a fallacy in my reasoning?

What you are doing is adding the velocity of the boat relative to the water to the velocity of the water relative to the ground, to get the velocity of the boat relative to the ground.

 

[vcsharp2003]

No. See below.
What you are doing is adding the velocity of the boat relative to the water to the velocity of the water relative to the ground, to get the velocity of the boat relative to the ground.

I think you've made a very good point. It's not a good idea to think that multiple velocities are trying to move an object else it might result in incorrect analysis and wrong answer.

 

[Lnewqban]

I guess if point P was not constrained by the strings in its motion but free to move like a boat in a flowing river (as mentioned in post#14), then we could have applied the concept of multiple velocities trying to guide it and added these multiple velocity vectors to get resultant velocity of point P. Is that correct?

You would need to do that in a non-symmetrical case, like $U_{left}>U_{right}$ for example.
Note that a velocity vector is always associated to only one frame of reference.

For the moving point, there is only one velocity vector respect to that frame.
Respect to a second frame of reference, you may assign a different velocity vector to the same point.

The classic cases of a boat in a flowing river and an airplane flying in a cross-wind, there are two frames of reference.
One frame is the fluid and a second frame is the ground.

One observer from the fluid can only see a forward movement of the boat or the airplane (V point respect to fluid).
Another observer from the ground can see the movement of the fluid respect to the ground (V fluid respect to ground).

That second observer can also see the movement of the boat or airplane respect to the ground, which is the vectoral addition of both velocities (V point respect to ground).

In the same way, an observer from the ground will see a linear vertical movement of our point P.
Another observer from the pulley, who is rotating with it, will see a string that rotates respect to the other pulley and to the ground.
At the same time, he/she will see point P getting closer to him/her in a curvilinear movement respect to the ground.

For our point P, the left string and the left pulley, we have a combination of two velocity vectors creating the vertical movement respect to the ground.
One is the instantaneous velocity vector U respect to the pulley.
The other one is the instantaneous vector Vt, which is the tangential velocity with which point P rotates CCW around the axis of the left pulley.
Both are instantaneous vectors because their magnitude and/or direction change at each instant.
The vectoral addition of those two instantaneous vectors forms our V instantaneous vector.

 

[vcsharp2003]

It helps to consider an extreme case. As θ approaches π/2, what happens to the relative values of u and v?

If we use $v \, cos{\theta} = U$ approach, then as θ approaches π/2, v will increase since component of v along string needs to be a constant U. So, as θ is increasing, the velocity of point P is increasing.

 

[haruspex]

If we use $v \, cos{\theta} = U$ approach, then as θ approaches π/2, U will approach 0 and also v will approach 0 since component of v along string will become smaller. So, as θ is increasing, the velocity of point P is decreasing.

But I asked about relative values, i.e. what happens to the ratio of U to v?

 

[vcsharp2003]

But I asked about relative values, i.e. what happens to the ratio of U to v?

Actually, v will increase since U is constant. The ratio of U to v will approach 0.

 

[haruspex]

Actually, v will increase since U is constant. The ratio of U to v will approach 0.

Right. And does that accord with what you would expect?

 

[vcsharp2003]

Right. And does that accord with what you would expect?

If mass m has an upward acceleration then yes velocity increase of mass is expected. But, honestly I am just going by the equation we have and concluding based on that equation. Is there any other way to expect in this situation?But looking at it from a common sense perspective, when $\theta = \dfrac {\pi} {2}$ then v should instantly reduce to 0 since the string cannot really keep going at U speed when there is no part of string left to be moved over the pulley.

 

[haruspex]

Is there any other way to expect in this situation?

You should be able to imagine it well enough for it to be obvious that when the strings between the pulleys are nearly horizontal

But looking at it from a common sense perspective, when $\theta = \dfrac {\pi} {2}$ then v should instantly reduce to 0 since the string cannot really keep going at U speed when there is no part of string left to be moved over the pulley.

For any given finite tension in the vertical strings, the upward momentum of the mass would ensure it continues beyond the equilibrium position. It could easily go beyond $\theta = \dfrac {\pi} {2}$ because of the huge mechanical advantage it has in that position.

 

[vcsharp2003]

It could easily go beyond θ=π2 because of the huge mechanical advantage it has in that position.

If the ends of strings over the pulley are being pulled down by something, then in horizontal position the point of junction P should not move, even though the hanging mass M should keep moving up beyond horizontal position till the string holding M becomes taut again.

 

[Steve4Physics]

Hi @vcsharp2003. I suspect the root of your problem is understanding why ‘v=ucosθ’ is wrong. Maybe this will help.

Crude diagram of left side:

A.B

...P​

P = moving point (P moves vertically upwards.with speed v)
A = top of pulley (a fixed point) Approximate AP to a straight line.
B = a fixed point above P and level with A, to give a right-triangle
θ = ∠APB

AP is the sloping section of the string.

AP gets shorter at a rate equal to u. But AP also rotates about A.
If AP didn't rotate about A, then ucosθ would be the vertical component of P’s velocity – but then P couldn’t rise purely vertically and the left and right strings couldn't remain joined.

We could say something like:
v = ucosθ + {some expression to allow for the rotation of AP about A}
but that would be a clumsy way to find v.

 

[haruspex]

If the ends of strings over the pulley are being pulled down by something, then in horizontal position the point of junction P should not move, even though the hanging mass M should keep moving up beyond horizontal position till the string holding M becomes taut again.

It does not matter how finitely taut you make a string, it can still vibrate.

 

[vcsharp2003]

It does not matter how finitely taut you make a string, it can still vibrate.

Yes, that's true. So, mass M will keep vibrating about horizontal position