Discussion Overview
The discussion revolves around the pressure drop experienced by a fluid flowing through a pipe, specifically under laminar viscous flow conditions. Participants explore the mechanics of pressure differences, forces acting on the fluid, and the implications of viscosity on flow behavior.
Discussion Character
- Exploratory
- Technical explanation
- Debate/contested
- Mathematical reasoning
Main Points Raised
- Some participants assert that a pressure difference between the ends of the pipe creates a net force that drives the fluid flow, while questioning whether this is a cause-and-effect relationship.
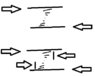
- Others discuss the role of viscous friction and shear stress, noting that these forces act against the pressure forces and affect the flow dynamics.
- A participant mentions that the velocity profile of the fluid transitions from uniform to parabolic as it flows downstream, suggesting that this affects the pressure distribution.
- Some participants propose that momentum transport in the transverse direction contributes to the pressure drop, although there is uncertainty about the mechanics involved.
- There are differing views on whether the model of fluid flow assumes that only the center of the fluid is being pushed, with some questioning the validity of this assumption.
- Mathematical expressions are provided to illustrate force balances and shear stresses within the fluid, indicating a technical approach to understanding the pressure drop.
- Concerns are raised about the clarity of pressure measurement and the implications of guesses made by participants, highlighting the complexity of the topic.
Areas of Agreement / Disagreement
Participants express a range of views on the mechanics of pressure drop, with no clear consensus reached. Some agree on the role of viscous forces, while others challenge the assumptions underlying the models discussed.
Contextual Notes
Participants note that the discussion involves assumptions about steady-state flow and the influence of upstream conditions on downstream behavior. There are also references to mathematical derivations that may not be fully interpreted, indicating potential gaps in understanding.
Who May Find This Useful
This discussion may be of interest to those studying fluid dynamics, particularly in the context of laminar flow and the effects of viscosity on pressure and flow behavior in pipes.