How Does the Rotational Inertia Affect Rolling Motion on an Inclined Plane?

[ILOVEPHYSIC]

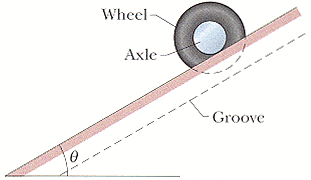
A uniform wheel of mass 14.0 kg is mounted rigidly on a massless axle through its center, as shown in the figure below. The radius of the axle is 0.200 m, and the rotational inertia of the wheel-axle combination about its central axis is 0.600 kg·m2. The wheel is initially at rest at the top of a surface that is inclined at angle θ = 30.0° with the horizontal; the axle rests on the surface while the wheel extends into a groove in the surface without touching the surface. Once released, the axle rolls down along the surface smoothly and without slipping. The wheel-axle combination moves down the surface by 3.00 m.

(a)Determine its rotational kinetic energy at this point? J

(b) Determine its translational kinetic energy at this point? J

Mgh= 1/2mw^2 + 1/2mv^2 --(1)
v=wR --(2)
The problem i feel confused is that what is R for since part of the wheel is inside the groove. I am not sure the question is just simply sub (2) into (1) and find the answer.

 

[Doc Al]

Mgh= 1/2mw^2 + 1/2mv^2 --(1)

Fix the first term on the right hand side, for rotational KE. (Should be I, not m.)

The problem i feel confused is that what is R for since part of the wheel is inside the groove.

What matters is what surfaces are in contact with each other. It's the axle that is touching the surface of the incline. The fact that the part of the wheel is in the groove is irrelevant.

 

[ILOVEPHYSIC]

Fix the first term on the right hand side, for rotational KE. (Should be I, not m.)What matters is what surfaces are in contact with each other. It's the axle that is touching the surface of the incline. The fact that the part of the wheel is in the groove is irrelevant.

Sorry for typing wrong in rotational KE. But the axle and wheel should move with same angular speed. Why don't wheel slow down the rotational motion?

 

[Doc Al]

But the axle and wheel should move with same angular speed.

They do!

Why don't wheel slow down the rotational motion?

The wheel does slow down the rotational motion, but that is reflected in the rotational inertia. The relationship v = ωr is the condition for rolling without slipping; the "r" is the distance from the surface to the center, which is the radius of the axle, not the wheel.