zippeh
- 12
- 0
Homework Statement
Suppose that the climber has mass m, has a center of gravity at a distance L1 from her feet, and holds the rope at a distance L2 from her feet. The climber rappels down a vertical cliff with her body raised θ1 above the horizontal. The rope makes an angle θ2 with the cliff face. Use the ‘usual’ coordinate system with +x to the right, +y up, and +z out-of-page. On the climber’s feet, call the horizontal and vertical components of the contact force H(vector) and V(vector) and begin by initially guessing that V (vector) points up. Give and expression for (a) the net force in the x-direction, (b) the net force in the y-direction, and (c) the net torque with respect to her feet. Solve for (d) the tension, (e) H, and (f) V.[/B]
Homework Equations
∑F=0 (since there is no movement)
∑τ=0 (since there is no movement)
The Attempt at a Solution
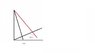
This is my issue currently. Since all the values are arbitrary, then there is a scenario with the angles. For example, if the tension force makes an acute angle with respect to the angled climber then the same angle "formula" to determine the perpendicular force on the radius (we are treating the radius as the climber's body) would not be the same if the force makes an obtuse angle with respect to the angled climber. Picture included to explain what I mean. (the tension angle can vary because length of the body can vary since every value is arbitrary). Thank in advance for your time!
To better explain what I am doing, since the tension force is at an angle, and the body is at an angle, I am finding the perpendicular component of the tension force with respect to the angled body. I hope this makes sense (since τ = R(vector) x F(vector)). I know I could also find the perpendicular radius component with respect to the force, but that would require the chosen force to be able to make a right triangle with the rotational point, which it can only do if the value is acute. Thanks! [/B]