How does unbalanced tension affect the motion of a rope?

[Alex126]

Homework Statement

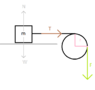
There is a block of known mass m on a horizontal surface. The block is connected to a pulley via a rope. The other end of the rope is pulled vertically, downwards, with a known force F. The pulley has a known moment of inertia I and radius r.
Calculate the acceleration a of the block.

Homework Equations

ΣM = I*α
α = angular acceleration = a/r (a = tangential acceleration)
ΣF = m*a (F = forces acting on a body)
M = r*F

The Attempt at a Solution

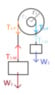
This would be the drawing, though I'm a bit unsure about that Tension force T:

Anyhow, I wrote the equation for the forces acting on the body, ignoring the Y axis since it's balanced:
+T = m*a

Then there is the other part of the problem, which focuses on the angular momenti on the pulley. Since the rotation is obviously clockwise, I'll call + the clockwise one, and - the counterclockwise one. Now, I know that there is a M_F, since clearly that force exists and so does its momentum, but is there also another force to consider, namely the tension T? If I think about it, there shouldn't be any other momentum, since that force F is the only actual force applied to the pulley, BUT surely the same force would make the pulley rotate differently if the mass m was also different: no mass -> same F should make the pulley go "faster"; plenty enough mass -> no motion at all.

Instinctively, I thought there should be something like this:
+M_F - M_T = I*α
Rationally, I don't know where this "-T" comes from. The "T" I drew quite clearly goes in the same direction as F, so if anything it should be +M_T. But then again, on the bottom part of the rope (where I drew F) maybe there is also a counter-Tension T₂ (equal in magnitude to the T I wrote, but pointing upwards, i.e. opposing the motion), and that's the one producing that -M_T.

The procedure after this point is straightforward, since I can just use the various equations with M_F = r*F and M_T = r*T, and a = α*r, combine them all in a system with T and α and get to the solution. What goes in the system, that's the question.

 

[haruspex]

The "T" I drew quite clearly goes in the same direction as F,

Tension (and likewise compression) is not a force, exactly. It is more like pairs of opposing forces.
If a string is under tension T, then at each point of the string there is a force T pulling away from the point in each direction.
If you were to draw separate free body diagrams for mass and pulley then they should show a T pointing away from the body in each case.

 

[Alex126]

Yea, got it. I think.
So if I drew the diagram only for the block, it would show these three forces: Weight, Normal force, and a Tension pointing to the right.
For the pulley, there would be two forces: F pointing down, and T pointing to the left.

The T from the block and the T from the pulley have the same magnitude, right?

If that's the case, then T = m*a (where this "T" is the one pointing to the right, when I isolate the first body) should have been correct, from earlier.

Likewise, for the Momentum relative to the pulley, the two forces playing a role here would be the F and the T which points to the left. Therefore, as I guessed earlier, the momenti were indeed +M_F - M_T = I*α

So this becomes:
1) r*F - r*T = I*a/r
2) T = m*a
=> r*F - r*m*a = I*a/r =>
=> r*F = a (r*m+I/r) => a = r*F/(r*m+I/r)

Is this it?

 

[haruspex]

The T from the block and the T from the pulley have the same magnitude, right?

In this case, yes. When would they not be the same? Hint: draw a free body diagram for that section of rope.

a = r*F/(r*m+I/r)

Yes.

 

[Alex126]

Ok, thanks for the answers.

When would they not be the same? Hint: draw a free body diagram for that section of rope.

That's kinda what was bothering me, because I was thinking of other kinds of exercises. One in particular had two "concentric overlapping discs of pulleys" (I'm sure there is a better term to indicate this, but I don't know it) with two blocks hanging on either side. The two discs of the pulley system rotated together with the same angular velocity. It looked something like this:

Here T_1-M is the tension T₁ for the body, and it's equal (or rather, opposite) to T_1-P which is the "counter-Tension" T₁ from the "pulley's point of view". Same thing with T₂, but T₂ is different from T₁. In this exercise we knew m₁, m₂, r₁, r₂, and the moment of inertia I (for some reason called J) of the "whole pulley" (i.e. considering the two discs as one object). I did this exercise basically the same way, except there were a few more things:
(m₁ > m₂, so assume counterclockwise rotation)
1) [First Body] +W₁ - T_1-M = m₁*a₁
2) [Second Body] -W₂ + T_2-M = m₂*a₂
3) [Pulley] +r₁*T_1-P - r₂*T_2-P = I*α
4/5) a₁ = α*r₁ ; a₂ = α*r₂

Here T₁ and T₂ were different, surely. Though I'm not sure this is the example you meant, since it's quite a bit far from the previous exercise :D

 

[haruspex]

Though I'm not sure this is the example you meant,

No, my question was when would a rope under tension exert a greater force at one end than at the other?

 

[Alex126]

I guess when there is something else pulling on the other side...? Something like friction on the table maybe?

 

[haruspex]

I guess when there is something else pulling on the other side...? Something like friction on the table maybe?

No. Bear in mind that in your question the system is accelerating. Draw a free body diagram for such a section of rope and consider the net force on it.

 

[Alex126]

Oh, well, if there was no block then :D

 

[haruspex]

Oh, well, if there was no block then :D

No, there is no block to consider in my question. There is just a straight length of rope with a greater tension at one end than at the other. What normally happens if there are unbalanced forces on an object?