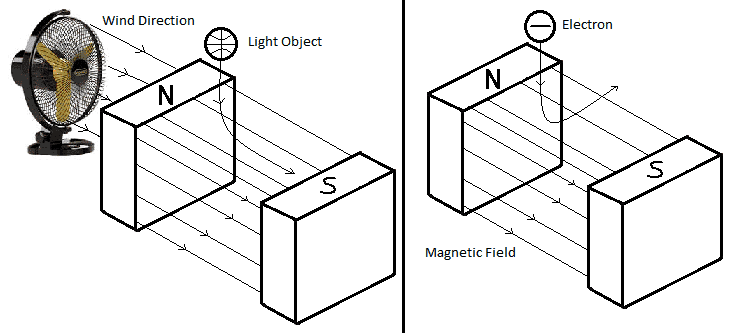
Electrons are deflected in a magnetic field due to the Lorentz force, which is calculated using the equation F = q(v × B), where F is the force, q is the charge, v is the velocity, and B is the magnetic field. The force acts perpendicular to both the velocity of the electron and the magnetic field, resulting in a change in direction rather than speed. This perpendicular force causes the electron to follow a helical path in a uniform magnetic field, maintaining a constant speed while changing direction. An analogy to mechanical forces, like pushing a table, is misleading since a magnetic field does not exert a direct push but rather alters the trajectory of charged particles. For example, using q = 1 C, v = 1 m/s, and B = 1 T results in a force of 1 N acting forward on the charge.