mathewings
- 8
- 0
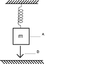
A block is susoended from the end of a spring. The spring is hanging off the ceiling. An external force holds the block so that, initially, the spring is not stretched or compressed. When the block is released, it oscillates up and down between positions A and B. If the mass of the block is 0.5kg and the spring constant is 10N/m, how far will the block fall when it is released?
I've tried equating gravitational potential and spring potential energy, but the height of the block can't be determined. I don't believe there's enough information to isolate a velocity to find kinetic energy. I'm fairly certain I'm on the right track in that I need to use conservation of energy. Any suggestions would be appreciated.
I've tried equating gravitational potential and spring potential energy, but the height of the block can't be determined. I don't believe there's enough information to isolate a velocity to find kinetic energy. I'm fairly certain I'm on the right track in that I need to use conservation of energy. Any suggestions would be appreciated.