How Far Does a Box Slide Down an Inclined Plane to Compress a Spring?

[domo]

Homework Statement

(My textbooks are in french, so I'm translating, might get some terms wrong.. )


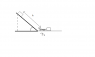
Starting from rest, a box of 31kg slides down a ramp inclined at an angle of 31 degrees, relative to the horizontal. At the bottom, the box hits a spring with a constant of 9.8 * 10^2N/m. The spring undergoes a compression of 0.26m before the box immobilizes. Determine the total distance that the box travelled, consider the friction negligible.

Homework Equations

Et1 = Et2
F = -kx
Ee = 1/2kx^2
Ec = 7/2mv^2

The Attempt at a Solution

I really can't find out how to determine the distance the box traveled. I know that i have to start out off by finding the amount of force it takes to compress the spring by 0.26m. But I have no idea how to do the rest. Any help would be very much apreciated :)

 

[CAF123]

Draw a sketch of the problem. The mass is released from rest from some height above the horizontal, moving down the incline and ultimately coming to rest because of the spring force which retards subsequent motion. Write energy conservation to relate the initial and final states of the system, introducing variables for the height above the ground where the mass started and the displacement of the spring.

 

[STEMucator]

Use $E_G = E_K$.

Then use $E_K = E_E$.

So really $E_G = E_E$.

Was there a height given in the question?

 

[domo]

The height was not given in the question, that's what really stumped me because I cannot calculate Eg..

 

[CAF123]

The height was not given in the question, that's what really stumped me because I cannot calculate Eg..

The height of the mass above the ground does not need to be specified numerically - the angle with the horizontal is enough. You can relate the height of the mass above the ground to the distance it travels down the slope via simple trigonometry.

 

[domo]

The height of the mass above the ground does not need to be specified numerically - the angle with the horizontal is enough. You can relate the height of the mass above the ground to the distance it travels down the slope via simple trigonometry.

I'm sorry, I just really don't understand how I'm supposed to solve this question. A bit more help would be appreciated. I'm clueless right now

 

[STEMucator]

I'm sorry, I just really don't understand how I'm supposed to solve this question. A bit more help would be appreciated. I'm clueless right now

I believe this question is missing information.

 

[domo]

I believe this question is missing information.

It is not :(, my textbook was able to come up with an answer for a similar question, just with different variables. Is it possible that all that I have to find is the height, using conservation of energy; then from there use sin to find the length hypotenuse? This seems to simple.

For example;

= Eg1+Ek1+Ee1 = Eg2+Ek2+Ee2
= Eg1 = Ee2
= mgh = 1/2kx^2
= (31 * 9.81)h = 0.5(8.9*10^2)(0.3)^2
= 304.11h = 40.05
= h = 0.132m

Now I can simply do

0.132/sin29 = 0.272m which would be my answer?
This question is not in my textbook therefore I have no way in checking if this answer is legitimate..

 

[CAF123]

I'm sorry, I just really don't understand how I'm supposed to solve this question. A bit more help would be appreciated. I'm clueless right now

See the attached sketch. The mass travels down the slope a distance h and then the spring is compressed a distance x. The box is shown like a rigid body for clarity, for purposes of the problem represent the box as a point particle (i.e with all the mass concentrated at the centre of mass) What is the energy of the system before it is released? What is the energy of the system when the box is at rest after the full compression of the spring?

Relate these via energy conservation and solve for h.

 

[domo]

See the attached sketch. The mass travels down the slope a distance h and then the spring is compressed a distance x. The box is shown like a rigid body for clarity, for purposes of the problem represent the box as a point particle (i.e with all the mass concentrated at the centre of mass) What is the energy of the system before it is released? What is the energy of the system when the box is at rest after the full compression of the spring?

Relate these via energy conservation and solve for h.

What you said makes sense, however the spring is a part of the slope, therefore it's not separately attached like your sketch

 

[STEMucator]

What you said makes sense, however the spring is a part of the slope, therefore it's not separately attached like your sketch

If the question is as such: http://gyazo.com/3ba5fb4ac8d8f775df1955a1f38593ff

Then information is missing. This can be observed by simply trying to relate the information:

$sin(31°) = \frac{h}{d+0.26m}$

Where $d$ is the unknown distance. One equation with two unknowns isn't going to help.

 

[CAF123]

From the wording of the question;

At the bottom, the box hits a spring...

I interpret this to mean that the spring is on the horizontal and not the slope. Note that the solution you posted in #8 was exactly what I had in mind.

What you said makes sense, however the spring is a part of the slope, therefore it's not separately attached like your sketch

 

[STEMucator]

From the wording of the question;I interpret this to mean that the spring is on the horizontal and not the slope. Note that the solution you posted in #8 was exactly what I had in mind.

Your diagram in post #9 is incorrect unfortunately. Think about it, the way you've defined the height has an x direction to it... which is wrong. Wouldn't that mean there would always be gravitational energy even though the height was zero? We both know this is impossible.

 

[CAF123]

Hi Zondrina,

Your diagram in post #9 is incorrect unfortunately. Think about it, the way you've defined the height has an x direction to it... which is wrong. Wouldn't that mean there would always be gravitational energy even though the height was zero? We both know this is impossible.

Just because the solution in #8 used h as the vertical distance of the box above the ground does not mean I have to use this letter to! Instead I denote hsinθ as the vertical - I.e what I can write is $$mg(h \sin \theta) = \frac{k}{2}x^2 \Rightarrow h = \frac{k x^2}{2mg \sin \theta}$$

 

[STEMucator]

Hi Zondrina,

Just because the solution in #8 used h as the vertical distance of the box above the ground does not mean I have to use this letter to! Instead I denote hsinθ as the vertical - I.e what I can write is $$mg(h \sin \theta) = \frac{k}{2}x^2 \Rightarrow h = \frac{k x^2}{2mg \sin \theta}$$

I see what you're thinking, but regardless of letter naming conventions it still doesn't work. You're simply saying:

$sin(\theta) = \frac{o}{h} \Rightarrow o = hsin(\theta)$.

The problem is, the hypotenuse is not given. So any further computations would be useless taking this route.

Also, the problem with the formula you've gotten for $h$ is that you're trying to find the distance (namely $x$), not the hypotenuse.

$h = \frac{k x^2}{2mg \sin \theta}$

Both $x$ and $h$ are unknown. One equation with two unknowns will not help.

 

[nasu]

If the question is as such: http://gyazo.com/3ba5fb4ac8d8f775df1955a1f38593ff

Then information is missing. This can be observed by simply trying to relate the information:

$sin(31°) = \frac{h}{d+0.26m}$

Where $d$ is the unknown distance. One equation with two unknowns isn't going to help.

You forget the physics of the problem.
The conservation of energy will allow to calculate the height or some related quantity (depends on notation).

 

[CAF123]

The problem is, the hypotenuse is not given.

Exactly, the hypotenuse is what we need to find.

Both $x$ and $h$ are unknown. One equation with two unknowns will not help.

x is not an unknown, it is the displacement of the spring.