How Fast Does a Pulse Travel Along a Steel Wire?

Thread starter momogiri
Start date Nov 9, 2007
Tags

String Wave

AI Thread Summary

A wave pulse travels along a steel wire in 24.0 milliseconds, with the wire's mass being 60.0 grams. The speed of the wave depends on the tension in the wire and its linear mass density, represented by the formula √(T/μ). The discussion highlights the need to understand these factors to calculate the wave speed accurately. The initial uncertainty about tackling the problem is resolved by referencing the appropriate formula. Understanding the relationship between tension and mass density is crucial for determining wave speed in this context.

Nov 9, 2007

momogiri

Problem
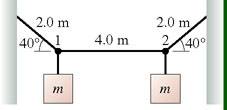
The figure shows two masses hanging from a steel wire. The mass of the wire is 60.0 g. A wave pulse travels along the wire from point 1 to point 2 in 24.0 ms.

Attempt
None yet, I don't really know how to tackle this :/

Physics news on Phys.org

Nov 9, 2007

Dick

Science Advisor

Homework Helper

What does the speed of a wave traveling down a wire depend on? Look it up.

Nov 9, 2007

momogiri

Ohh ok, so by using \sqrt{\frac{T_{N}}{\mu}}, I can find it :D
Thanks for your help

Thread 'Rolling without slipping on a curved surface'

Kindly see the attached pdf. My attempt to solve it, is in it. I'm wondering if my solution is right. My idea is this: At any point of time, the ball may be assumed to be at an incline which is at an angle of θ(kindly see both the pics in the pdf file). The value of θ will continuously change and so will the value of friction. I'm not able to figure out, why my solution is wrong, if it is wrong .

View full post »

Thread 'I've come across another fluid pressure problem I don't understand'

Neglect gravity other than that of water; neglect friction. F1=ρgsh=1000*10*1*(1+4)=50000 N; F1=ρgsh=1000*10*0.1*4=4000 N; F3=50000-4000=46000 N?

View full post »

Thread 'Struggling to understand the concept of this question (ice cube in water optics question)'

TL;DR Summary: I came across this question from a Sri Lankan A-level textbook. Question - An ice cube with a length of 10 cm is immersed in water at 0 °C. An observer observes the ice cube from the water, and it seems to be 7.75 cm long. If the refractive index of water is 4/3, find the height of the ice cube immersed in the water. I could not understand how the apparent height of the ice cube in the water depends on the height of the ice cube immersed in the water. Does anyone have an...

View full post »