How fast is the lighthouse beam moving along the shoreline?

[karush]

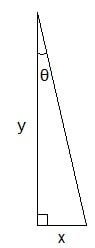
A light in a lighthouse $1$ km offshore from a straight shoreline is rotating at $2$ revolutions per minute.

How fast is the beam moving along the shoreline when it passes the point $\frac{1}{2}$ km from the point opposite the lighthouse?

ok we have a right triangle where the $\theta$ is the angle of the beam from the shore
and we have $2$ revolutions per minute is the same as $\displaystyle\frac{4\pi}{min}$

so we have ($y$ being the dist from the lighthouse to the shore)
$\displaystyle \text{y}=\tan{\theta}$

the rev thing is what ? me

 

[MarkFL]

Let's generalize a bit and derive a formula we can then plug our data into.

The first thing I would do is draw a diagram:

View attachment 2681

As we can see, we may state:

\(\displaystyle \tan(\theta)=\frac{x}{y}\)

Now, let's differentiate with respect to time $t$, bearing in mind that while $x$ and $\theta$ are functions of $t$, $y$ is a constant. What do you get?

 

[karush]

$\frac{DX}{DT}=\sec^2{\theta}\frac{d\theta}{DT}$

 

[MarkFL]

$\frac{DX}{DT}=\sec^2{\theta}\frac{d\theta}{DT}$

That's close, but what about the constant $y$?

 

[karush]

how bout $\frac{dx}{dt}=(1+x^2 )∙4\pi$ since $\frac{d\theta}{dt}=4\pi$

 

[MarkFL]

Yes, if we write:

\(\displaystyle x=y\tan(\theta)\)

then differentiate with respect to time $t$, we find:

\(\displaystyle \d{x}{t}=y\sec^2(\theta)\d{\theta}{t}\)

Now, by Pythagoras, we know:

\(\displaystyle \sec^2(\theta)=\tan^2(\theta)+1=\frac{x^2+y^2}{y^2}\)

And so we have:

\(\displaystyle \d{x}{t}=\frac{x^2+y^2}{y}\d{\theta}{t}\)

Now we just have to plug in the given data...:D

 

[karush]

\(\displaystyle \sec^2(\theta)=\tan^2(\theta)+1=\frac{x^2+y^2}{y^2}\)

And so we have:

\(\displaystyle \d{x}{t}=\frac{x^2+y^2}{y}\d{\theta}{t}\)

Now we just have to plug in the given data...:D

$\displaystyle\frac{{\left(\frac{1}{2}\right)^2 + 1}}{1}=\frac{5}{4}$ so then $\displaystyle\frac{5}{4}\cdot 4\pi = 5\pi \frac{km}{min}$