a.a
- 126
- 0
Homework Statement
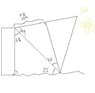
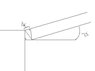
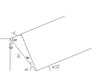
Radio waves of wavelength 250 meters from a star reach a radio telescope by two separate paths. One is a direct path to the receiver which is situated on the edge of a cliff by the ocean. The second is by reflection off the water. The first minimum of destructive interference occurs when the star is 25 degrees above the horizon. Find the height of the cliff.
We know the path difference is 125 meters since first minimum occurs at 25 degrees, so the difference is half a wavelength.
I just found phase difference (=half wavelength) and found path difference (from: phase difference = 2pi*phase difference/wavelength)
Then I used height = phase difference*sin theta
but that didnt work
any advice