tartio
- 5
- 0
Homework Statement
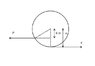
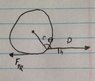
A uniform sphere of radius r and weight W slides
along the floor due to a constant horizontal force P applied by a
string. Suppose the coefficient of friction is µ. Find the height of the
string above the floor h.
Homework Equations
ƩT = 0 because there cannot be non-zero torque as the sphere must not roll, as it is sliding.
T = r x F
Friction = μ*W
The Attempt at a Solution
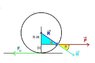
ƩT = 0 = T(P) + T(Friction)
= r x P + r x F(Friction)
= rPsinθ + rF(Friction)
= rPsinθ + rμW
=> -rPsinθ = rμW
=> sinθ = -(μW/P)
I have it to the definition of the angle of the force applied, but how do I relate the angle to the height above the ground?