The first step in this proof is to define free-fall acceleration, which is the rate of change of velocity for an object in free-fall due to gravity. In this case, the object is the glass ball and the acceleration is caused by the Earth's gravity.
Next, we can use the definition of acceleration, which is the change in velocity over time, to find the equation for free-fall acceleration. In this case, we can use the equation a=(v_f-v_i)/t, where v_f is the final velocity, v_i is the initial velocity, and t is the time interval.
Since the ball is thrown straight up and then falls back down, the initial velocity and final velocity will be the same, but in opposite directions. Therefore, we can rewrite the equation as a=(v_f-(-v_f))/t, which simplifies to a=(2v_f)/t.
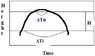
Now, we need to find a way to relate the time intervals ΔTl and ΔTu to the final velocity v_f. This is where the distance between the two levels, H, comes into play. We can use the equation for average velocity, which is v_avg=Δx/Δt, where Δx is the change in distance and Δt is the change in time.
In this case, the change in distance is H, and the change in time is ΔTl for the first pass and ΔTu for the second pass. This gives us v_avg=H/ΔTl and v_avg=H/ΔTu.
Since the final velocity is the same for both passes, we can set these two equations equal to each other and solve for v_f, giving us v_f=H(ΔTl+ΔTu)/(ΔTlΔTu).
Now, we can plug this value for v_f into our equation for acceleration, giving us a=(2H(ΔTl+ΔTu))/(ΔTlΔTu).
Finally, we can use algebra to manipulate this equation into the desired form of g=(8H)/(ΔTl^2-ΔTu^2). First, we can multiply both the numerator and denominator by 2, giving us a=(4H(ΔTl+ΔTu))/(2ΔTlΔTu). Then, we can use the difference of squares formula to