soupastupid
- 34
- 0
Unwinding Cylinder--Dynamics
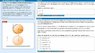
A cylinder with a moment of inertia I (about its axis of symmetry), mass m, and radius r has a massless string wrapped around it which is tied to the ceiling (Intro 1 figure) .
At time t=0 the cylinder is released from rest at height h above the ground. Use g for the magnitude of the acceleration of gravity. Assume that the string does not slip on the cylinder. Let v_vec represent the instantaneous velocity of the center of mass of the cylinder, and let omega_vec represent the instantaneous angular velocity of the cylinder about its center of mass. Note that there are no horizontal forces present, so for this problem
v_vec = -v(y-hat) and omega_vec = - omega(z-hat)
Torque = I(angular_acceleration)
F= m(linear_acceleration)
I'm having trouble with part B
T is the tension of the spring
if I goes to zero, the object will be turning faster in the -z direction.
The tension of the spring does less work on its rotation and more work on its linear momentum.
and so
If the T went to 0, then linear a should be g right?
because the tension does no work on either the angular and linear momentum and so the cylinder will just fall right?
the answer is the second choice
right?
if T went to infinity, then there would not be acceleration in the in the -y direction.
so if T went to infinity, a should be zero right?
if T equaled mg then linear acceleration would also be zero because the forces of the weight and T cancel out
right?
Homework Statement
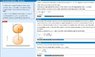
A cylinder with a moment of inertia I (about its axis of symmetry), mass m, and radius r has a massless string wrapped around it which is tied to the ceiling (Intro 1 figure) .
At time t=0 the cylinder is released from rest at height h above the ground. Use g for the magnitude of the acceleration of gravity. Assume that the string does not slip on the cylinder. Let v_vec represent the instantaneous velocity of the center of mass of the cylinder, and let omega_vec represent the instantaneous angular velocity of the cylinder about its center of mass. Note that there are no horizontal forces present, so for this problem
v_vec = -v(y-hat) and omega_vec = - omega(z-hat)
Homework Equations
Torque = I(angular_acceleration)
F= m(linear_acceleration)
The Attempt at a Solution
I'm having trouble with part B
T is the tension of the spring
if I goes to zero, the object will be turning faster in the -z direction.
The tension of the spring does less work on its rotation and more work on its linear momentum.
and so
If the T went to 0, then linear a should be g right?
because the tension does no work on either the angular and linear momentum and so the cylinder will just fall right?
the answer is the second choice
right?
if T went to infinity, then there would not be acceleration in the in the -y direction.
so if T went to infinity, a should be zero right?
if T equaled mg then linear acceleration would also be zero because the forces of the weight and T cancel out
right?