How is the Minkowski 4-space equation connected to hyperbolic functions?

[stevmg]

The standard Minkowski 4-space equation runs like this (as far as I know);

x'² + y'² + z'² - c²t'²= x² + y² + z² - c²t²

For purposes of simplicity, if we drop the y and z components and go to a 2-space, let c = 1 and x measured in units of c (if we express c as 300M m/sec, the 1 unit for x would be 300,000,000 m,( we would get
x'² - t'² = x² - t² which is equivalent to a general algebraic equation:
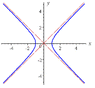
x² - t² = a²
In the process of that derivation, the \gamma's "drop out."

This leads to an equation of symmetric hyperbola where (x,0) = (\pm a,0)

In terms of the general equaltion of a symmetric hyperbola there should be a constant, say
b₁ under the x and a second constant, say b₂ under the t, however Einstein et al have assigned 1 for both those values.

I have derived algebraically this equation using the Lorentz transforms - it does work out.

How do I relate the \gamma from the Lorentz transforms [1/\sqrt[]{(1 - v^2)/c^2}] back to the a²? There is a relation which would change the a² for different v's (or different \gamma 's) but is "lost in translation." How do I get it back? This would make relating this hyperbolic equation back to hyperbolic trig functions more intuitive and thus explain the hyperbolic function matrix for the Lorentz Transformation more intuitive.

 

[Daverz]

There isn't a relationship between the gamma here, which is in the Lorentz transformation that relates the two frames, and a^2, because a^2 is an invariant (the square of the interval). If you think of vectors in the Euclidean plane, there's no relation between the length of a vector and the angle between two coordinate systems that have been rotated about the origin.

 

[stevmg]

I probably asked the question incorrectly, so I'll modify it thus:

Clearly, the c'²t'² - x'² = c²t² - x² represents different points for different x's and t's with respect to two specific frames of reference in which, by custom the S' frame is moving at v wrt to S frame (or inertial frame which is arbitrarily assigned.)

Thus, for a given relationship of two frames S and S' with S' moving at v, say we have the equation c²t² - x² = a²

So, for whatever a is in this situation, if we have the S frame steady and another FR S" which moves at v" wrt S we will still have this new relation based on c²t² - x² = a² which will be different that the original pair and the only way it can differ is in the a. It is the v that determines the value of \gamma. This, the \gamma, call it \gamma' for the first pair of FR's (S and S') will be different than the \gamma for the second pair of FR's), call it \gamma"

There must be some relation between the a² and the \gamma's.

 

[bapowell]

If I understand what you're doing properly, a^2 is an invariant under Lorentz transformations, i.e. we understand the hyperbola to be the orbit of the Lorentz group. The points of the hyperbola correspond to the same physical coordinates as perceived by a progression of observers each boosted infinitesimally relative to the next. So we boost (apply a Lorentz transformation with a specific \gamma) to move from one point on the hyperbola to another. By varying v from 0 to c (\gamma from 1 to infinity), we trace out the whole hyperbola.

 

[stevmg]

Over my head here.

Is that true? Is the hyperbola traced out by different gamma's or v's (as you look at it?)

I guess that it is traced out dependent on the a's, as the x and t values, once the gamma is calculated (it is known from the given v,) are both linear. (x' is linearly related to x and t and t' is linearly related to x and t) - kind of makes sense in the idea of a ongoing translation of axes.

Also, makes sense that if the gamma had any play in the original equation (the a's) I gave (from Einstein, et al,) then it wouldn't dop out as we derived the 4-space equation from the Lorentx transforms.

Let me know... is the hyperbola gamma dependent? I now don't think so. So, where does the a come from? What does it mean?

 

[yossell]

I guess I too am a bit confused at what you're getting at, so sorry if this is worse than useless...

Clearly, the c'2t'2 - x'2 = c2t2 - x2 represents different points for different x's and t's with respect to two specific frames of reference in which, by custom the S' frame is moving at v wrt to S frame (or inertial frame which is arbitrarily assigned.)

I would say they represent the SAME spacetime point. Take a coordinate system, O. Take an arbitrary event in that coordinate system, E. Suppose in O its got coordinates (t, x). If you like, put a^2 = c^2t^2 - x^2 - but remember, the event is arbitrary. Then, in any other coordinate system O' (with the same origin), whatever its velocity wrt O, if the *same* event has coordinates (t' x') in O', then c^2t'^2 - x'^2 = a^2 also.

So a is to a large part arbitrary - it just depends on the event you chose. It's the *invariance* of a, the fact that the value of this function of the coordinates of one and the same event comes out the same - even when we change our coordinate systems.

 

[stevmg]

I guess I too am a bit confused at what you're getting at, so sorry if this is worse than useless...


I would say they represent the SAME spacetime point. Take a coordinate system, O. Take an arbitrary event in that coordinate system, E. Suppose in O its got coordinates (t, x). If you like, put a^2 = c^2t^2 - x^2 - but remember, the event is arbitrary. Then, in any other coordinate system O' (with the same origin), whatever its velocity wrt O, if the *same* event has coordinates (t' x') in O', then c^2t'^2 - x'^2 = a^2 also.

So a is to a large part arbitrary - it just depends on the event you chose. It's the *invariance* of a, the fact that the value of this function of the coordinates of one and the same event comes out the same - even when we change our coordinate systems.

That's good as your answer isn't useless. Remember I have no one here to bounce things off for simple concepts and, as a result, a "brain fart" actually gets posted - by me. I forgot that those transformation formulas actually referred to the same point or event but just looked at from different FR's (hence the v and gamma.) If we were face to face and I brought it up you would have corrected the BF in one instant.

I'm just working through some basic concepts here - remember - nobody here to talk to about these, you folks are it.

Staying within the "two-space" it looks like that Minkowski equation means that for any given point in space-time the a² is the same regardless of what FR you choose. This would mean a an infinite set of gamma's (or velocities of FR's)for each point as they all would satisfy the a². Note that x's and t's for a given point do fall on a hyperbola wrt that point.

Am I right so far?

Remember, what is useless to you isn't so to me as I do learn and I do build on what you say...

I never would have been able to teach medical students and interns if I thought their questions were useless.

 

[bapowell]

Over my head here.
Let me know... is the hyperbola gamma dependent? I now don't think so. So, where does the a come from? What does it mean?

Sorry for the jargon. Each point along the hyperbola corresponds to a different value of \gamma, so it's not quite correct to say that they are independent. In fact, as the hyperbola asymptotes to the 45 degree line, the speed of the observer is asymptoting to v = c.

The a is the most important geometric quantity in special relativity. It is often referred to as the space-time interval, or the 'invariant length' (even though it's not necessarily a spatial length). Physically, it is the proper time. This should make sense -- an observer's proper time is, after all, independent of his state of motion.

 

[bapowell]

Staying within the "two-space" it looks like that Minkowski equation means that for any given point in space-time the a² is the same regardless of what FR you choose. This would mean a an infinite set of gamma's (or velocities of FR's)for each point as they all would satisfy the a². Note that x's and t's for a given point do fall on a hyperbola wrt that point.

Am I right so far?

Yes! The invariance of a^2 embodies the relativity principle. It's essentially Minkowski's geometric interpretation of the Einstein postulates. The Lorentz transformations are those mathematical transformations that leave the a^2 invariant. For each a^2 there are an infinite set of x's and t's -- each of these are referring to the same physical spacetime point -- they are the coordinates of this same point as measured by different observers all moving at different speeds.

 

[stevmg]

Sorry for the jargon. Each point along the hyperbola corresponds to a different value of \gamma, so it's not quite correct to say that they are independent. In fact, as the hyperbola asymptotes to the 45 degree line, the speed of the observer is asymptoting to v = c.

The a is the most important geometric quantity in special relativity. It is often referred to as the space-time interval, or the 'invariant length' (even though it's not necessarily a spatial length). Physically, it is the proper time. This should make sense -- an observer's proper time is, after all, independent of his state of motion.

Yes! The invariance of a^2 embodies the relativity principle. It's essentially Minkowski's geometric interpretation of the Einstein postulates. The Lorentz transformations are those mathematical transformations that leave the a^2 invariant. For each a^2 there are an infinite set of x's and t's -- each of these are referring to the same physical spacetime point -- they are the coordinates of this same point as measured by different observers all moving at different speeds.

Yes, Yes, Yes - we are home! Now, how do we get the a's. If one were given a particular x and t, one could then calculate the corresponding a, I suppose.

What I am working is the geometric interpretation from a hyperbolic function point of view what I've posted above (see .jpg post above in post 1
https://www.physicsforums.com/showpost.php?p=2810273&postcount=1
on the Minkowski hyperbolic function matrix.)

 

[yossell]

Now, how do we get the a's. If one were given a particular x and t, one could then calculate the corresponding a, I suppose.

It sounds as if this isn't good enough for you. Can you give us some idea of what else you might have hoped for?

From the geometric point of view, you might just regard the fact that the separation (the Minkowski 'distance') between two events is just a primitive geometric, coordinate-independent fact, just like the classical fact that two points of space are n metres apart, irrespective of any coordinate system.

What I am working is the geometric interpretation from a hyperbolic function point of view what I've posted above (see .jpg post above in post 1
https://www.physicsforums.com/showpost.php?p=2810273&postcount=1
on the Minkowski hyperbolic function matrix.)

Not sure what you're hoping for here - can you expand? The jpg looks like a coordinate transform. The geometric approach is normally thought of as a coordinate free way of thinking about relativity. Of course, at some point, coordinates and geometry have to be related, but could you say a little more about what you're trying to do.

 

[yuiop]

The Minkowski transformation of coordinates is given by:

\begin{bmatrix}ct&#039;\\ x&#039;\\ y&#039;\\ z&#039;\end{bmatrix}=<br /> \begin{bmatrix}<br /> \gamma &amp; -\beta\gamma &amp; 0 &amp; 0\\ <br /> -\beta\gamma &amp; \gamma &amp; 0 &amp; 0\\ <br /> 0 &amp; 0 &amp; 1 &amp; 0\\ <br /> 0 &amp; 0 &amp; 0 &amp; 1<br /> \end{bmatrix}<br /> \begin{bmatrix}ct\\ x\\ y\\ z\end{bmatrix}

where \beta = v/c and \gamma = 1/sqrt{(1-\beta^2)}

If we define a parameter \phi = -\ln[\gamma(1-\beta)] (sometimes called the rapidity) then it can be shown mathematically that:

\gamma = \cosh \phi

and

\beta\gamma = \sinh \phi

so the Minkowski transformation can also be written as:

\begin{bmatrix}ct&#039;\\ x&#039;\\ y&#039;\\ z&#039;\end{bmatrix}=<br /> \begin{bmatrix}<br /> \cosh \phi &amp; -\sinh \phi &amp; 0 &amp; 0\\ <br /> -\sinh \phi &amp; \cosh \phi &amp; 0 &amp; 0\\ <br /> 0 &amp; 0 &amp; 1 &amp; 0\\ <br /> 0 &amp; 0 &amp; 0 &amp; 1<br /> \end{bmatrix}<br /> \begin{bmatrix}ct\\ x\\ y\\ z\end{bmatrix}

and your original equation can be written as:

a^2 = x&#039;^2 - ct&#039;^2 = (\cosh \phi \ x - \sinh \phi \ ct)^2 \ - (\cosh \phi \ ct - \sinh \phi \ x)^2

\Rightarrow a^2 = \cosh^2 \phi \ x^2 \ -2\cosh \phi \sinh \phi \ xct \ + \sinh^2 \phi \ c^2t^2 \ - \cosh^2 \phi \ c^2t^2 \ +2 \cosh \phi \sinh \phi \ xct \- \sinh^2 \phi \ x^2

\Rightarrow a^2 = \cosh^2 \phi \ x^2 \ + \sinh^2 \phi \ c^2t^2 \ - \cosh^2 \phi \ c^2t^2 - \sinh^2 \phi \ x^2

\Rightarrow a^2 = (\cosh^2 \phi -\sinh^2 \phi) x^2 \ + (\sinh^2 \phi - \cosh^2 \phi) c^2t^2

and from http://en.wikipedia.org/wiki/Hyperbolic_function#Useful_relations"

\Rightarrow a^2 = x^2 - c^2t^2

 

[yossell]

It must be past my bedtime - I don't understand any of kev's post.edit: now i look like an idiot coz kev changed his post!

 

[yuiop]

It must be past my bedtime - I don't understand any of kev's post.

Actually, it must be past my bedtime. I think I made a complete hash of the first part, so I have deleted that part, while I think about it some more.

 

[DrGreg]

It must be past my bedtime - I don't understand any of kev's post.

[STRIKE]Well, the second half makes sense, but I've no idea why he chose to write

<br /> x^2 - c^2t^2 = c^2<br />​

That makes no sense for an arbitrary event (t,x).[/STRIKE]

EDIT: strike out comment that refers to material now deleted from kev's post.

 

[yuiop]

Well, the second half makes sense, but I've no idea why he chose to write

<br /> x^2 - c^2t^2 = c^2<br />​

That makes no sense for an arbitrary event (t,x).

Yep, your right. See my last post. Oops!

I think what I meant to say was something like:

the Minkowski metric is:

<br /> x^2 - c^2t^2 = c^2\tau^2<br />​

Since both c and the proper time \tau are both invariant under transformation to another frame, then the RHS must be invariant and so the LHS must also be invariant under transformation. Since steve effectively wrote:

<br /> x^2 - c^2t^2 = a^2<br />​

the quantity (a) must also be invariant. I am tired, so I might have made more mistakes. (Apologies in advance).

 

[stevmg]

The Minkowski transformation of coordinates is given by:

\begin{bmatrix}ct&#039;\\ x&#039;\\ y&#039;\\ z&#039;\end{bmatrix}=<br /> \begin{bmatrix}<br /> \gamma &amp; -\beta\gamma &amp; 0 &amp; 0\\ <br /> -\beta\gamma &amp; \gamma &amp; 0 &amp; 0\\ <br /> 0 &amp; 0 &amp; 1 &amp; 0\\ <br /> 0 &amp; 0 &amp; 0 &amp; 1<br /> \end{bmatrix}<br /> \begin{bmatrix}ct\\ x\\ y\\ z\end{bmatrix}

where \beta = v/c and \gamma = 1/sqrt{(1-\beta^2)}

If we define a parameter \phi = -\ln[\gamma(1-\beta)] (sometimes called the rapidity) then it can be shown mathematically that:

\gamma = \cosh \phi

and

\beta\gamma = \sinh \phi

so the Minkowski transformation can also be written as:

\begin{bmatrix}ct&#039;\\ x&#039;\\ y&#039;\\ z&#039;\end{bmatrix}=<br /> \begin{bmatrix}<br /> \cosh \phi &amp; -\sinh \phi &amp; 0 &amp; 0\\ <br /> -\sinh \phi &amp; \cosh \phi &amp; 0 &amp; 0\\ <br /> 0 &amp; 0 &amp; 1 &amp; 0\\ <br /> 0 &amp; 0 &amp; 0 &amp; 1<br /> \end{bmatrix}<br /> \begin{bmatrix}ct\\ x\\ y\\ z\end{bmatrix}

and your original equation can be written as:

a^2 = x&#039;^2 - ct&#039;^2 = (\cosh \phi \ x - \sinh \phi \ ct)^2 \ - (\cosh \phi \ ct - \sinh \phi \ x)^2

\Rightarrow a^2 = \cosh^2 \phi \ x^2 \ -2\cosh \phi \sinh \phi \ xct \ + \sinh^2 \phi \ c^2t^2 \ - \cosh^2 \phi \ c^2t^2 \ +2 \cosh \phi \sinh \phi \ xct \- \sinh^2 \phi \ x^2

\Rightarrow a^2 = \cosh^2 \phi \ x^2 \ + \sinh^2 \phi \ c^2t^2 \ - \cosh^2 \phi \ c^2t^2 - \sinh^2 \phi \ x^2

\Rightarrow a^2 = (\cosh^2 \phi -\sinh^2 \phi) x^2 \ + (\sinh^2 \phi - \cosh^2 \phi) c^2t^2

and from http://en.wikipedia.org/wiki/Hyperbolic_function#Useful_relations"

\Rightarrow a^2 = x^2 - c^2t^2

It must be past my bedtime - I don't understand any of kev's post.


edit: now i look like an idiot coz kev changed his post!

Actually, it must be past my bedtime. I think I made a complete hash of the first part, so I have deleted that part, while I think about it some more.

Yep, your right. See my last post. Oops!

I think what I meant to say was something like:

the Minkowski metric is:

<br /> x^2 - c^2t^2 = c^2\tau^2<br />​

Since both c and the proper time \tau are both invariant under transformation to another frame, then the RHS must be invariant and so the LHS must also be invariant under transformation. Since steve effectively wrote:

<br /> x^2 - c^2t^2 = a^2<br />​

the quantity (a) must also be invariant. I am tired, so I might have made more mistakes. (Apologies in advance).

1) Everyone of you hit on it

<br /> x^2 - c^2t^2 = a^2<br />​

\begin{bmatrix}ct&#039;\\ x&#039;\\ y&#039;\\ z&#039;\end{bmatrix}=<br /> \begin{bmatrix}<br /> \gamma &amp; -\beta\gamma &amp; 0 &amp; 0\\ <br /> -\beta\gamma &amp; \gamma &amp; 0 &amp; 0\\ <br /> 0 &amp; 0 &amp; 1 &amp; 0\\ <br /> 0 &amp; 0 &amp; 0 &amp; 1<br /> \end{bmatrix}<br /> \begin{bmatrix}ct\\ x\\ y\\ z\end{bmatrix}

where \beta = v/c and \gamma = 1/sqrt{(1-\beta^2)}


\gamma = \cosh \phi

and

\beta\gamma = \sinh \phi

so the Minkowski transformation can also be written as:

\begin{bmatrix}ct&#039;\\ x&#039;\\ y&#039;\\ z&#039;\end{bmatrix}=<br /> \begin{bmatrix}<br /> \cosh \phi &amp; -\sinh \phi &amp; 0 &amp; 0\\ <br /> -\sinh \phi &amp; \cosh \phi &amp; 0 &amp; 0\\ <br /> 0 &amp; 0 &amp; 1 &amp; 0\\ <br /> 0 &amp; 0 &amp; 0 &amp; 1<br /> \end{bmatrix}<br /> \begin{bmatrix}ct\\ x\\ y\\ z\end{bmatrix}

a^2 = x&#039;^2 - ct&#039;^2 = (\cosh \phi \ x - \sinh \phi \ ct)^2 \ - (\cosh \phi \ ct - \sinh \phi \ x)^2

\Rightarrow a^2 = \cosh^2 \phi \ x^2 \ -2\cosh \phi \sinh \phi \ xct \ + \sinh^2 \phi \ c^2t^2 \ - \cosh^2 \phi \ c^2t^2 \ +2 \cosh \phi \sinh \phi \ xct \- \sinh^2 \phi \ x^2

\Rightarrow a^2 = \cosh^2 \phi \ x^2 \ + \sinh^2 \phi \ c^2t^2 \ - \cosh^2 \phi \ c^2t^2 - \sinh^2 \phi \ x^2

\Rightarrow a^2 = (\cosh^2 \phi -\sinh^2 \phi) x^2 \ + (\sinh^2 \phi - \cosh^2 \phi) c^2t^2

and from http://en.wikipedia.org/wiki/Hyperbolic_function#Useful_relations"

\Rightarrow a^2 = x^2 - c^2t^2

2) You must all be English as you talk of 11 PM GMT as being past your bedtime when it is 6 PM (1800) here.

I was trying to find the relationship between a and \phi.

I know that sinh \phi = ct/a and cosh \phi = x/a

I haven't gotten to the:

\phi = -\ln[\gamma(1-\beta)]

yet

Now I have to let the dust settle, have you all agree what I just wrote was correct, and to do some problems with rapidity which is used in acceleration/deceleration situations.

I had to learn hyperbolic geometry and I haven't seen that since college (c. 1960), so give me a bloody break (again, I am assuming you are all English, otherwise I would have chosen a few New York present participles.)

Steve G

 

[yuiop]

It must be past my bedtime - I don't understand any of kev's post.


edit: now i look like an idiot coz kev changed his post!

Nah.. I'm the idiot. You were right that my post did not make sense the first itme around, but by the time I realized my blunder and tried to cover my tracks it was too late and DrGreg had imortalised my mistake

 

[stevmg]

I was trying to find the relationship between a and \phi.

I know that sinh \phi = ct/a and cosh \phi = x/a

I haven't gotten to the:

\phi = -\ln[\gamma(1-\beta)]

Steve G

Hey, while you boys were in la-la land, help me out...

Is what I wrote correct?

stevg

 

[yuiop]

1)
I was trying to find the relationship between a and \phi.

I know that sinh \phi = ct/a and cosh \phi = x/a

I haven't gotten to the:

\phi = -\ln[\gamma(1-\beta)]

yet

My knowledge of hyperbolic functions is probably worse than yours. I have to refer to Wikipedia to remind me of the rules, but I think I have figured it out.

x^2 - c^2t^2 = a^2 defines (a) as imaginary number because for a particle moving at less than the speed of light x^2 &lt; c^2t^2. It is better to write:

a^2 = (c\delta t)^2 -\delta x^2

a = \sqrt{(c\delta t)^2 -\delta x^2}

This is basically using the +--- convention for the metric, rather than the -+++ convention we were using before and I am using differentials because I want to deal with velocities rather than coordinate points.

Now given cosh (\phi) = \pm \ \delta x/a

(recall that \cosh (-\phi) = \cosh (+\phi))

I will use the negative root from now on, because it is more convenient and define a function f such that:

f = \cosh (\phi) = \frac{-\delta x}{a} = \frac{-\delta x}{\sqrt{c^2\delta t^2-\delta x^2}} = \frac{-\delta x/(c\delta t)}{\sqrt{1 - \delta x^2/(c\delta t)^2}} = \frac{-\beta}{\sqrt{1-\beta^2}}

Now using the definition

\textrm{sech}(\phi) = \frac{1}{\cosh(\phi)}

I define another function (g) such that

g = \text{sech}(\phi) = \frac{1}{f} = \frac{\sqrt{1-\beta^2}}{-\beta}

The inverse sech function is defined as:

\text{asech} (g) = \pm \ln\left(\frac{1+\sqrt{1-g^2}}{g}\right)

\Rightarrow \phi = \pm \ln\left (\frac{1+\sqrt{1+(1-\beta^2)/\beta^2}}{(\sqrt{1-\beta^2})/(-\beta)}\ \right)

\Rightarrow \phi = \pm \ln\left (\frac{-\beta+\sqrt{\beta^2+(1-\beta^2)}}{\sqrt{1-\beta^2}}\ \right)

\Rightarrow \phi = \pm \ln\left (\frac{-\beta +1}{\sqrt{1-\beta^2}}\right)

\Rightarrow \phi = \pm \ln(\gamma(1-\beta))

==========================

You could of course take the simpler route and use the relation:

f = \cosh(\phi) = \gamma = 1/\sqrt{1-\beta^2}

and work from there.

There is also the relation:

e^{\phi} = \cosh(\phi) + sinh(\phi) = x/a +ct/a

\Rightarrow \phi = \ln(x/a + ct/a)

that might prove useful.

See http://en.wikipedia.org/wiki/Hyperbolic_function

As you have probably already noticed, using rapidity because of the sinplicity of adding velocities, rather than using the relativistic addition equation, introduces a world of pain involving hyperbolic functions, exponential functions and imaginary or complex numbers to handle.

Applogies in advance for any typos, I was just outlining some basic methods that might help.

 

[starthaus]

Hey, while you boys were in la-la land, help me out...

Is what I wrote correct?

stevg

It is really simple:

cosh(\phi)=\gamma

But

cosh(\phi)=1/2(e^\phi+e^{-\phi})

From the above you get an equation degree 2:

e^{2\phi}-2\gamma*e^\phi+1=0

with two roots

e^{\phi1}=\gamma(1+\beta)

e^{\phi2}=\gamma(1-\beta)

So:

\phi1=ln(\gamma(1+\beta))
\phi2=ln(\gamma(1-\beta))

 

[starthaus]

==========================

You could of course take the simpler route and use the relation:

\gamma = \sqrt{1-\beta^2}

Not.

 

[yuiop]

You could of course take the simpler route and use the relation:

f = \cosh(\phi) = \gamma = 1/\sqrt{1-\beta^2}

and work from there.

After fixing the typo pointed out by Starthaus in the above, you can continue like this:

\phi = \pm \textrm{acosh}(f) = \pm \ln(f +\sqrt{f^2-1}) = \pm \ln(\gamma + \sqrt{\gamma^{-2}-1})= \pm \ln(\gamma + \gamma \beta)

\qquad \ = \pm \ln(\gamma (1+\beta))

which is the other solution.

It is worth noting that:

\cosh(\phi) = \gamma = 1/\sqrt{1-\beta^2}

implies

\cosh(\phi) = \frac{1}{\sqrt{1-dx^2/(cdt)^2}}= \frac{cdt}{\sqrt{(cdt)^2 - dx^2}} = \frac{cdt}{a}

which differs from the \cosh(\phi) = dx/a that you gave earlier, but it is just possible that both solutions are correct.

My guess is that

\phi = \ln(\gamma (1+\beta)) \Rightarrow cdt/a

and

\phi = -\ln(\gamma (1-\beta)) \Rightarrow x/a

but I have not verified that.

 

[starthaus]

After fixing the typo pointed out by Starhaus in the above, you can continue like this:

\phi = \textrm{acosh}(f) = \pm \ln(f +\sqrt{f^2-1}) = \pm \ln(\gamma + \sqrt{\gamma^{-2}-1})= \pm \ln(\gamma + \gamma \beta^2)

\qquad \ = \pm \ln(\gamma (1+\beta^2))

Not. This is incorrect. The correct solution is:

\phi=ln(\gamma(1\pm\beta))

My guess is that

\phi = \ln(\gamma (1+\beta^2)) \Rightarrow cdt/a

and

\phi = -\ln(\gamma (1-\beta^2)) \Rightarrow x/a

but I have not verified that.

Not.

 

[stevmg]

It is really simple:

cosh(\phi)=\gamma

But

cosh(\phi)=1/2(e^\phi+e^{-\phi})

From the above you get an equation degree 2:

e^{2\phi}-2\gamma*e^\phi+1=0

with two roots

e^{\phi1}=\gamma(1+\beta)

e^{\phi2}=\gamma(1-\beta)

So:

\phi1=ln(\gamma(1+\beta))
\phi2=ln(\gamma(1-\beta))

Well, I guess I was close but no cigar.

I keep forgetting that we have to use the ct axis as the "y" axis which would invert my answer your answer. I know, x² - c²t² in timelike area is negative, leading to answers so we must use c²t² - x²

I was trying to keep a geometric feel for all this so that when I delve into rapidity I could visualize what I was doing.

Also, why is this matrix referred to as a rotation of axes? What is rotated?

 

[stevmg]

BTW - writing in LaTeX sucks. The Preview Post option sucks too brings in extraneous data. What is needed is a "draft" mode like there is in many web-based e-mails do that one can see what they are sending before it is sent and appropriate adjustments are made. It is harder than hell to try to interpret LaTeX and make any sense out of what is being posted.

Just a suggestion.

stevng

 

[yuiop]

So:

\phi1=ln(\gamma(1+\beta))
\phi2=ln(\gamma(1-\beta))

Wikipedia gives:

\phi1=ln(\gamma(1+\beta))
\phi2=-ln(\gamma(1-\beta))

http://en.wikipedia.org/wiki/Lorentz_transformation

There seems to a problem with way you obtain your two roots. Something is not right, but I can not put my finger on it at the moment.

 

[stevmg]

I like the Wikipedia answer quotes because that's my answer, too but I'll give eve money that starthaus is right. I never have seen him miss before.

 

[Fredrik]

BTW - writing in LaTeX sucks. The Preview Post option sucks too brings in extraneous data.

What it does is to show the wrong image sometimes, an older image instead of the new one. This is a known bug. It's annoying, but easy to work around. Just refresh and resend after each preview, and you will see exactly what your post will look like.

 

[yossell]

Kev and stevmg

which bit of the wiki page are you looking at to get those answers for phi1 and phi2? I could see something close-ish, under the rapidity section, but I couldn't quite see that formula.

I think it's just a matter of applying the quadratic formula for roots of a quadratic equation to
<br /> e^{2\phi}-2\gamma*e^\phi+1=0<br />

i.e. letting x = e^{\phi}, substituting, and solving, to get Starhaus' two solutions for \phi.

 

[starthaus]

Wikipedia gives:

\phi1=ln(\gamma(1+\beta))
\phi2=-ln(\gamma(1-\beta))

http://en.wikipedia.org/wiki/Lorentz_transformation

There seems to a problem with way you obtain your two roots. Something is not right, but I can not put my finger on it at the moment.

You are reading the wiki page wrong, there is no \phi1 and \phi2 in the wiki solution. Wiki author gets only one of the two roots since:

-ln(\gamma(1-\beta))=ln(\gamma(1+\beta))Either way, your answer is clearly wrong. I can see that you surreptitiously changed the \beta^2 into \beta after I flagged the error. This is good but you should let people know when you correct your errors.

 

[starthaus]

Kev and stevmg

which bit of the wiki page are you looking at to get those answers for phi1 and phi2? I could see something close-ish, under the rapidity section, but I couldn't quite see that formula.

I think it's just a matter of applying the quadratic formula for roots of a quadratic equation to
<br /> e^{2\phi}-2\gamma*e^\phi+1=0<br />

i.e. letting x = e^{\phi}, substituting, and solving, to get Starhaus' two solutions for \phi.

Yes, of course, basic math. The wiki page gets only one of the two solutions.

 

[yuiop]

You are reading the wiki page wrong, there is no \phi1 and \phi2 in the wiki solution. Wiki author gets only one of the two roots since:

-ln(\gamma(1-\beta))=ln(\gamma(1+\beta))

Yep, I did misread that part.

This means your two roots are effectively:

\phi1=ln(\gamma(1+\beta)) = -ln(\gamma(1-\beta))
\phi2=ln(\gamma(1-\beta)) = -ln(\gamma(1+\beta))

so we could say:

\phi = \pm ln(\gamma(1+\beta)) \textrm{ or } \pm ln(\gamma(1-\beta))

and we can equally say:

\phi = ln(\gamma(1\pm\beta)) \textrm{ or } - ln(\gamma(1\pm\beta))

so there appears to be some ambiguity in the logarithmic definition of \phi

 

[starthaus]

Yep, I did misread that part.

This means your two roots are effectively:

\phi1=ln(\gamma(1+\beta)) = -ln(\gamma(1-\beta))
\phi2=ln(\gamma(1-\beta)) = -ln(\gamma(1+\beta))

so we could say:

\phi = \pm ln(\gamma(1+\beta)) \textrm{ or } \pm ln(\gamma(1-\beta))

and we can equally say:

\phi = ln(\gamma(1\pm\beta)) \textrm{ or } - ln(\gamma(1\pm\beta))

so there appears to be some ambiguity in the logarithmic definition of \phi

There is no ambiguity, algebraic equations degree 2 tend to have two different solutions.

 

[DrGreg]

For a given velocity (β) there is only one possible rapidity (φ), so Wikipedia is right. Of course for a given Lorentz factor (γ) there are two possible values of β, positive and negative, which is where the confusion has arisen here.

In the context quoted, γ is to be regarded as a function of β rather than the other way round.

 

[yuiop]

Getting back to steve's original question:

I was trying to find the relationship between a and \phi.

I know that sinh \phi = ct/a and cosh \phi = x/a
...
...
Now I have to let the dust settle, have you all agree what I just wrote was correct...

From the above image, you can see that:

t^2 - x^2 = constant =a^2 = (cdt^2) -dx^2

Note that the constant is not necessarily one. The hyperbolic curve is the horizontal version that represents a curve of constant proper time for various relative velocites, rather than using the vertical version you were using before that represents a curve of constant proper disnance.

Now if we use the hyperbolic identity:

\cosh^2\phi - \sinh^2\phi = 1

we can say:

a^2(\cosh^2\phi- \sinh^2\phi) = (cdt)^2 - dx^2

\cosh^2\phi - \sinh^2\phi = \frac{(cdt)^2}{a^2} - \frac{dx^2}{a^2}

From the above it natural to make the association:

\cosh^2 \phi = \frac{(cdt)^2}{a^2}

\Rightarrow \cosh^2 \phi = \frac{(cdt)^2}{(cdt)^2 - dx^2} = \frac{1}{1-\beta^2} = \gamma^2

and

\sinh^2 \phi = \frac{dx^2}{a^2}

\Rightarrow \sinh^2 \phi = \frac{dx^2}{(cdt)^2 - dx^2} = \frac{\beta^2}{1-\beta^2} = \beta^2 \gamma^2

I was trying to keep a geometric feel for all this so that when I delve into rapidity I could visualize what I was doing.

Also, why is this matrix referred to as a rotation of axes? What is rotated?

If you look at the diagram below:

You can see that the x' axis has been rotated anticlockwise while the t' axis has been rotated clockwise relative to the x and t axes respectively. The amount of rotation of the axes depends on the relative velocity between the F and F' frames. The relative velocity in the above diagram is 0.6c so the proper time t' =1 translates to t=0.8 and the proper distance x' =1 translates to x=0.8. Note that point P = (x',t') = (0,1) remains on the horizontal hyperbola in the left diagram, for all relative velocities and the point P = (x',t') = 1,0) remains on the vertical hyperbola in the right diagram, for all relative velocities.

Diagrams from http://hubpages.com/hub/Minkowski-Diagram

 

[starthaus]

For a given velocity (β) there is only one possible rapidity (φ), so Wikipedia is right.

That would be \phi=arctanh(\beta) since tanh(\phi)=\beta

Of course for a given Lorentz factor (γ) there are two possible values of β, positive and negative, which is where the confusion has arisen here.

There is no confusion and there is no connection to the positive and negative \beta. The two solutions arise from the other definition of \phi, i.e.

\phi=arccsh(\gamma)

In the context quoted, γ is to be regarded as a function of β rather than the other way round.

True but it has nothing to do with the issue being discussed.

 

[Dale]

How do I relate the \gamma from the Lorentz transforms [1/\sqrt[]{(1 - v^2)/c^2}] back to the a²? There is a relation which would change the a² for different v's (or different \gamma 's) but is "lost in translation." How do I get it back?

Is this what you are asking:

dt^2 - dx^2 = -da^2 = d\tau^2

\frac{d\tau^2}{dt^2} = 1 - \frac{dx^2}{dt^2}

\frac{d\tau}{dt} = \sqrt{1 - v^2}

\gamma = \frac{dt}{d\tau} = \frac{1}{\sqrt{1 - v^2}}

 

[yuiop]

Wikipedia gives \varphi = artanh(\beta) = \ln\left(\frac{\sqrt{1-\beta^2}}{1- \beta} \right)= \ln\left(\frac{1}{\gamma(1-\beta)}\right)

so it would seem that the rapidity \varphi = arctanh(\beta)= 1/\phi. Curiously, Wikipedia defines both \phi and \varphi as the rapidity on different pages.

http://en.wikipedia.org/wiki/Rapidity

http://en.wikipedia.org/wiki/Lorentz_transformation

[EDIT]\varphi = arctanh(\beta) \ne 1/\phi. Slipped up again. See post 43.

 

[starthaus]

Wikipedia gives \varphi = artanh(\beta) = \ln\left(\frac{\sqrt{1-\beta^2}}{1- \beta} \right)= \ln\left(\frac{1}{\gamma(1-\beta)}\right)

so it would seem that the rapidity \varphi = arctanh(\beta)= 1/\phi. Curiously, Wikipedia defines both \phi and \varphi as the rapidity on different pages.

http://en.wikipedia.org/wiki/Rapidity

http://en.wikipedia.org/wiki/Lorentz_transformation

No, if you do the math carefully:

\varphi = \phi

 

[yuiop]

No, if you do the math carefully:

\varphi = \phi

Please demonstrate.

 

[starthaus]

Please demonstrate.

arctanh(\beta)=arccsh(\gamma)

Both wiki pages you cited say the same exact thing, you have just misread what they say.

 

[yuiop]

arctanh(\beta)=arccsh(\gamma)

Both wiki pages you cited say the same exact thing, you have just misread what they say.

Using the inverse hyperbolic function (http://en.wikipedia.org/wiki/Inverse_hyperbolic_function)

\varphi = \ln\left(\frac{1}{\gamma(1-\beta)}\right) = -\ln(\gamma(1-\beta)) = \ln(\gamma(1+\beta))

So DrGreg and Wikipedia are right when they say there is one unique solution to the rapidity when it is defined by \varphi, which is more tightly defined than \phi which has two solutions (as you have shown). There is a subtle difference.

Anyway, Steve. Are we any closer to answering your original question?

 

[starthaus]

Wikipedia gives \varphi = artanh(\beta) = \ln\left(\frac{\sqrt{1-\beta^2}}{1- \beta} \right)= \ln\left(\frac{1}{\gamma(1-\beta)}\right)

so it would seem that the rapidity \varphi = arctanh(\beta)= 1/\phi. Curiously, Wikipedia defines both \phi and \varphi as the rapidity on different pages.

http://en.wikipedia.org/wiki/Rapidity

http://en.wikipedia.org/wiki/Lorentz_transformation

[EDIT]\varphi = arctanh(\beta) \ne 1/\phi. Slipped up again. See post 43.

Yes, you have a hard time getting basic math right.

 

[stevmg]

To starthaus, kev, yossell, DrGreg, DaleSpam et al - You have all done yeoman's work in explaining this to me. I will have to now download all these posts so that I can read them on paper (easier to do than computer scree and I can jump back and forth between posts quicker.)

We need an area where we can put drafts of posts so that we can work on them (LaTeX is tedious) and not be forced to shove them onto the PF.

starthaus - It is not the Wikipage that is wrong, it is my brain that is wrong. Takes time to get my brain right - which it eventually does. I will have to download all these replies onto paper so I can peruse them and it will be easier to go back and forth between posts than it is on computer. I need to understand the hyperbolic relationships for me to understand your acceleration paper which uses this. Otherwise, it is just "monkey see, monkey do."

kev - how did you upload those graphics:

https://www.physicsforums.com/showpost.php?p=2812721&postcount=36:

without them appearing as thumbnails, as they did in my post:

https://www.physicsforums.com/showpost.php?p=2811664&postcount=17

I see you dowwnloaded them from a website, which I do not have, but I do have images. Are there any web-accessible programs or whatever to generate these kinds of graphs or did you get them from other web postings?

The vertical hyperbolas you posted - are they the usual hyperbolas associated with these kinds of problems. Surely, the asymptotic light cone is. Which way do we go? Up and down, or sideways? Don't make fun of me, now, and you all know what I mean.

I WILL eventually get this on a "cognitive" (internalized) level.

 

[yuiop]

kev - how did you upload those graphics:

https://www.physicsforums.com/showpost.php?p=2812721&postcount=36:

without them appearing as thumbnails, as they did in my post:

If you can find a suitable image on the web then right click on the image and select "properties" and copy the url address from there. Wrap the link address in [ img ] [ /img ] tags (without the spaces) or use the insert image feature in the PF post editing tools. If the images are made by you, then you need to post them on your own website or on a website like photobucket that let's you store images on the web. You can also upload images to your PF blog, open up the thumbnail to view it and grab the link address from the properties. (not sure if PF would encourage you to do this, as you would be using up their storage space, but it is technically possible )

 

[stevmg]

Here's one for the books, I hope, even if it's Mad Comic Books.

starthaus has stated and in books like Taylor/Wheeler 2nd ed Spacetime Physics it is stated that:

\exists a \phi such that cosh (\phi) = \gamma

Wherever I have read, that has sort of been a jump off assumption proven backwards by then showing consequences of that assumption to be true. To wit, v\gamma = sinh (\phi).

Now, what bugs the crap out of me is that I have never seen (not that I had such a great library at my disposal) an intuitive yet accurate demonstration that, in fact, the above assertion is directly true.

Without going to the e's \pm/2 etc. which are the standard textbook definitions of sinh and cosh it would be neat if we could have a geometric visualization of what a hyperbolic function is. I have attached a .pdf file scanned from a calculus review book, very thin, from 1959 which was first published in 1957 just such a demonstration in a file Hyperbolic functions.pdf. It is The Calculus by C.O. Oakley from the Barnes and Noble College Outline Series, pages 198-200. No plagiarism here as I am giving him (it is a he) full credit.

The hyperbolas in the graphs are of the form x² - y² = a². The foci of these hyperbolas are along the abscissa and these hyperbolas are symmetric. The positive x-intercept is at (a, 0). The coordinates of the foci are irrelevant for this discussion. By the Einstein-Minkowski 4-space equations:

x² - c²t² = x'² - c²t'² or x² - c2^t2 = a constant, say a²

This matches the equation in this textbook literally as is (if you use x for and ct for y).

From here on let us use c = 1 and v = \beta = "the old v"/c

Now, from that Oakley .pdf file \exists a \phi such that cosh (\phi) = x/a

If we look at \gamma we get \gamma = 1/(1 - v²)^(1/2)
Remember, I am using v instead of \beta because it is easier to type and in some textbooks v is used as a fraction of c.

This is "backwards" as this ratio has the constant (1) on the top and the variable [(1 - v²)^(1/2)] on the bottom.

That's easy to fix:

[1/[(1 - v²)^(1/2)]/[1/1] is still the same RATIO. Shortening it, we get
[1/[(1 - v²)^(1/2)]

substituting that for x
we get x² = [1/[(1 - v²)]. This is the same as \gamma² or "gamma squared"
and, in this case, a = 1 or a² = 1

Now that hyperbola is x² - y² = 1² = 1

y² = x² - 1

Moving on along

y² = [1/[(1 - v²)] - 1 = v²/[(1 - v²)]

or y = v/[(1 - v^2(1/2) = v\gamma or "v times gamma"

y also = sinh (\phi) from Oakley. So, now we have a geometric "proof" that \gamma = cosh (\phi) and
v\gamma or "v times gamma" = sinh (\phi).

From above, x = \gamma = [1/[(1 - v²)^(1/2)] = cosh (\phi)
Both of these are useful in the matrix multiplication representation of the Lorentz transformations.

From the algebra above we have shown that x²/1² - y²/1² = 1² or cosh² (\phi) - sinh² (\phi) = 1. This is a well known identity from hyperbolic trigonometry.

This reasoning above is not a tautology ("circular logic") because that same identity in hyperbolic trigonometry is proven in other ways (see Oakley, p. 200 in the attached .pdf)

 

[starthaus]

Here's one for the books, I hope, even if it's Mad Comic Books.

starthaus has stated and in books like Taylor/Wheeler 2nd ed Spacetime Physics it is stated that:

\exists a \phi such that cosh (\phi) = \gamma

Wherever I have read, that has sort of been a jump off assumption proven backwards by then showing consequences of that assumption to be true. To wit, v\gamma = sinh (\phi).

Now, what bugs the crap out of me is that I have never seen (not that I had such a great library at my disposal) an intuitive yet accurate demonstration that, in fact, the above assertion is directly true.

Yes, you have seen https://www.physicsforums.com/blog.php?b=1911 but you forgot. I showed you how tanh(\phi)=\beta is derived. This is equivalent with cosh(\phi)=\frac{1}{\sqrt{1-tanh^2(\phi)}}=\gamma.

 

[Dickfore]

If you differentiate x^{2} - c^{2} \, t^{2} = a^{2} with respect to t, considering x a function of t, then you ought to obtain:

<br /> 2 x \, \dot{x} - 2 \, c^{2} \, t = 0<br />

or

<br /> \beta \equiv \frac{\dot{x}}{c} = \frac{c \, t}{x}<br />

The definition of \gamma is:

<br /> \gamma = (1 - \beta^{2})^{-\frac{1}{2}} = \left[ 1 - \left(\frac{c \, t}{x}\right)^{2} \right]^{-\frac{1}{2}} = \left(\frac{x^{2} - c^{2} \, t^{2}}{x^{2}}\right)^{-\frac{1}{2}} = \frac{x}{a}<br />

 

[stevmg]

Getting back to steve's original question:
If you look at the diagram below:

You can see that the x' axis has been rotated anticlockwise while the t' axis has been rotated clockwise relative to the x and t axes respectively. The amount of rotation of the axes depends on the relative velocity between the F and F' frames. The relative velocity in the above diagram is 0.6c so the proper time t' =1 translates to t=0.8 and the proper distance x' =1 translates to x=0.8. Note that point P = (x',t') = (0,1) remains on the horizontal hyperbola in the left diagram, for all relative velocities and the point P = (x',t') = 1,0) remains on the vertical hyperbola in the right diagram, for all relative velocities.

Diagrams from http://hubpages.com/hub/Minkowski-Diagram

kev -

I cannot make heads, tails, x's, y's, t's or anything out of those diagrams.

I know Galilean transformations are "shear." That is - like a box squished to the left or right with non-perpendicular axes. Is that a form of rotation in itself? Or does the abscissa and ordinate axes remain perpendicular under Galilean transformations?

Is it the Lorentzian transformations that twist the ordinate axis off perpendicular to the x-axis?

This thumbnail (I still haven't figured out how to get a full sized picture uploaded) is what I am talking about. In this case, the y-axis is twisted or rotated off perpendicular.

If it were just a Galillean transformation, the y-axis would still be perpendicular but the "world lines" would be off perpendicular...

Am I right?

Remember, step-by-step I learn...