Benjamin_harsh
- 211
- 5
- Homework Statement
- Find the moment of this Force about point A.
- Relevant Equations
- ##M_{A} = - (1200.Sin 30^{0} X 140) + (1200.Cos 30^{0} X 140)##
A force of 1200N acts on a bracket as shown in the below figure. Find the moment of this Force about point A.
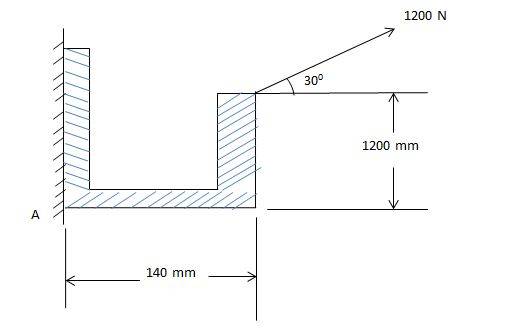
Taking moments of components of 1200N force about point A.
∴ ##M_{A} = - (1200.Sin 30^{0} * 140) + (1200.Cos 30^{0} * 140)##
##M_{A} = 40.71 X 10^{3} Nm##
I am confused, because Force 1200 is far away from A and also not touching each other. How is moment at A using Force 1200 is calculated? I am also confused with negative signs.
Taking moments of components of 1200N force about point A.
∴ ##M_{A} = - (1200.Sin 30^{0} * 140) + (1200.Cos 30^{0} * 140)##
##M_{A} = 40.71 X 10^{3} Nm##
I am confused, because Force 1200 is far away from A and also not touching each other. How is moment at A using Force 1200 is calculated? I am also confused with negative signs.
Last edited: