How Is the Net Moment Calculated in a Circular Disc?

[xunxine]

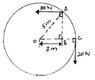
I understand that to find moment of force, we look at direction of force and perpendicular distance. In the diagram, O is the centre and pivot of the circular disc.

Would the anticlockwise moment at A be (30N x 4m)? I'm not sure if this is true, cos the distance 4m is only AB. It does not include O which is the pivot.
Should we resort to resolving the 30N force to 2 components at 5m (OA)?
(Clockwise moment is straightforward here, isn't it?)

 

[Doc Al]

Would the anticlockwise moment at A be (30N x 4m)?

Yes.

I'm not sure if this is true, cos the distance 4m is only AB. It does not include O which is the pivot.

What counts is the perpendicular distance from the line of the force to the pivot, which equals AB.

Should we resort to resolving the 30N force to 2 components at 5m (OA)?

That's a perfectly fine thing to do. Try it and you'll see that you get the same answer for the moment, since OA*F*sinθ = AB*F.

(Clockwise moment is straightforward here, isn't it?)

Sure.