I How is this a representation of a 3 dimensional torus?

[docnet]

TL;DR Summary

How is this expression of a torus?

In a differential geometry text, a torus is defined by the pair of equations:

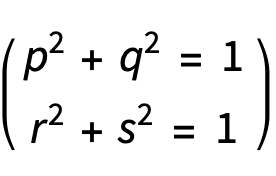
I initially thought this was somehow a torus embedded in 4 dimensions, but I do not see how we can visualize two orthogonal 2-dimensional Euclidian spaces. How is this a representation of a 2 dimensional torus embedded in 3 dimensions, with 4 presumably orthogonal coordinates?

 

[martinbn]

This is a two dimensional torus.

 

[Office_Shredder]

The idea is you can imagine a torus as a circle rotated around in a circle. The first equation defines your location on the first circle, and the second the second circle.

 

[mathwonk]

in 4 space with coords p,q,r,s, the subspaces p=q=0 and r=s=0 are two orthogonal euclidean 2 dimensional spaces. this torus meets each of them in a circle.

Alternatively, R^4 = R^2 x R^2 is the product of two orthogonal euclidean planes. your two equations define two (3 dimensional) "cylinders", one in each of these products, i.e. S^1 x R^2 and R^2 x S^1. Setting both equations equal to zero defines the intersection of these two cylinders, namely (S^1xR^2)intersect(R^2xS^1) = S^1xS^1.

 

[docnet]

thank you for your replies. It makes more sense now. It is a product of the sets {p^2+q^2=1} and {r^2+s^2=1}.