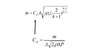I How long would it take for gas to leak out of a space box?

[Albertgauss]

I could not find an easy or believable source on this question on the internet. Anyway, if I had a box (volume V) in space full of gas (density N) and a hole suddenly appeared, how long would it take all of the air to completely leave the box out into space? I would assume the air would be at regular pressure P, temperature T, and made up of air density as normal on Earth. The hole in the box it leaks out would have area A. Even just pointing me to a good, basic, article would be helpful.

 

[phyzguy]

Give the temperature and pressure in the box, try calculating the number per second of gas atoms that strike an area A in a time dt. You can assume that any atom that hits the hole leaves the box. This will then give you dN/dt. Since you know the initial number N of atoms in the box, you can then write a differential equation that you can solve to get N(t). Since N will decay exponentially, it will take a very long time for all of the air to leave the box. You might want to rephrase your question to ask how long until the number of atoms in the box (or the pressure) drops below some value.

 

[JRMichler]

This is a fluid dynamics problem in choked flow. Here is a reference: https://en.wikipedia.org/wiki/Choked_flow. You need to treat the gas pressure in the box as a variable and integrate the resulting equation.

The fluid dynamic equations hold until the pressure gets so low that you need to consider the individual molecules.

 

[cjl]

Give the temperature and pressure in the box, try calculating the number per second of gas atoms that strike an area A in a time dt. You can assume that any atom that hits the hole leaves the box. This will then give you dN/dt. Since you know the initial number N of atoms in the box, you can then write a differential equation that you can solve to get N(t). Since N will decay exponentially, it will take a very long time for all of the air to leave the box. You might want to rephrase your question to ask how long until the number of atoms in the box (or the pressure) drops below some value.

Unless the hole is very small relative to the mean free path of the gas molecules, this will be incorrect. The interactions in the gas as it accelerates to sonic velocity in the throat of the orifice will significantly impact the answer. The correct way to do this is by using the equations JRMichler referenced above for choked flow.

 

[phyzguy]

Unless the hole is very small relative to the mean free path of the gas molecules, this will be incorrect. The interactions in the gas as it accelerates to sonic velocity in the throat of the orifice will significantly impact the answer. The correct way to do this is by using the equations JRMichler referenced above for choked flow.

I accept this, but I have a question. Is this true even if the wall of the box is very thin? In that case there is no "throat" really.

 

[JRMichler]

Google is your friend on wall thickness. Use search terms vena contracta orifice or orifice discharge coefficient. As a very rough approximation, if the wall of the box is thinner than the orifice diameter, it's thin enough that the thickness does not affect the flow rate. That's for a square edge orifice, where the upstream edge is a square corner.

 

[boneh3ad]

It seems several of you have stolen the answer I was going to give about choked flow. I will further add that, from the choked mass flow equation, the problem can be simplified to a first-order differential equation with constant coefficients for either mass or pressure remaining in the box. It's actually a fairly easy problem to solve for as long as the continuum assumption holds, and it's one that I like to give as homework or on exams to undergraduates when I teach compressible flow.

 

[Albertgauss]

Hi all,
I'm going to look at that article if "choked flow". I haven't been able to get to this until now. I am glad I waited a little while to check this, as there was a lot I realized I didn't even know to put into my question or that would matter. This is very helpful as I didn't know even where to start.

One thing I can clear up though: the wall of the box is very thick. I didn't realize that might make a difference. I didn't even know there was a category of physics called "choked flow" but I will look at that. Yes, I would assume "continuum", if I can take this term at face value. Also, I would assume the corners do not matter much, so it would be a fairly big box. Not sure how to express that here in the correct limits. Would it be easier if I made the box a sphere and got rid of the corners all together? Yes, I do expect that the temperature and pressure would change (as well as the density as the gas particles do leave the hole).

 

[boneh3ad]

"Choked flow" is not a category of physics. It's a concept (a rather small but important one) within the field of fluid mechanics.

 

[cjl]

I would tend to assume the shape of the box would not matter much (which should be true as long as the box is much larger than the hole). However, the thick wall will change things. How thick of a wall (relative to the hole diameter) are we talking here?

 

[Albertgauss]

Okay, I'm thinking about this. Let me assume, and see if this is right. The reason the thickness of the wall matters is that the flow of gas through the hole will be different whether the hole is just like an immediate opening into space (wide hole diameter much larger than thickness of wall), or pass through a kind of tunnel (thickness of box is much longer than the diameter of the hole) before the gas gets into space. These two scenarios will produce very different results, is this correct?

By contrast, for any side of the box away from the single hole, the thickness of the faces of the box should not matter, is this correct?

 

[cjl]

That is correct, yes. In the case of the tunnel scenario, there will be significant losses due to wall friction as it accelerates through the tunnel, resulting in a lower discharge compared to just a hole of the same diameter.

 

[Nidum]

Perhaps remember that free space far away from possible heat sources is extremely cold . Standard nozzle calculations probably won't give reliable answers to the question asked .

You might find it interesting to read about what was observed by the crew regarding the escaping oxygen after the tank exploded during the Apollo13 mission .

 

[cjl]

That depends on the environment and the container. Skylab lost power shortly after launch and became extremely hot, requiring a repair team to be sent up to prevent it from getting to a temperature that would melt the insulation on the wiring inside. That having been said, it would be worth checking the temperature in the throat when doing these calculations to make sure that the gas escaping the container wouldn't be condensing.

 

[Albertgauss]

Okay, I got the equation on the web-page. I uploaded a file of what I found. I already have a few questions.

The [C][/d], if I insert the bottom expression into the general mass flow equation, it looks like the mass flow rate cancels out. That doesn't make sense to me. That's the arrow I put in the slide.

Also, the "k" in the (k+1)/(k-1) term, wiki didn't define what that is. What quantity does this represent?

My eventual goal is to find out how long it takes for the Mass of the gas to go to zero.

I will start with the easiest scenario, where everything (or as much as can be) is constant. Can I assume, just to begin easy, that the upstream pressure is constant, the temp of the gas is constant, the hole diameter would be large compared to thickness of the wall where the gas exits. I will have the specific heats constant.

What would be the simplest type of opening? The choices appear to be an "Orifice Plate", a "de Laval nozzle", and a "rocket engine nozzle".

For the delta-P, what would be the easiest pressure drop across the constriction for the simplest math? Can this term be constant, to start out with?

Can the density of the gas be constant, for the easiest case? Seems like it can't, since gas is leaving the hole. It also seems that the density of the gas should be a function of time, linked to the mass flow rate. Since density is mass per unit volume, can I simply convert density into the mass divide by the Volume, but leave the Volume constant since the Volume would be the unchanging Volume of the box? That would leave me with a diff equation with dm/dt on the left and "m" raised to the negative one-half via the coefficient [C][/d] on the right-hand side. Is this right? If not, how do I fix it?

I think I got everything in that equation. Let me know if I missed something.

 

[Albertgauss]

Also, does anyone know of any videos that show actual choked-gas flows in progress?

 

[boneh3ad]

Perhaps remember that free space far away from possible heat sources is extremely cold . Standard nozzle calculations probably won't give reliable answers to the question asked .

That's not likely to be true. The flow at the throat is going to be sonic (by definition) so the upstream gas, which determines the flow rate, is going to be pretty much unaffected by the temperature outside the box. Once the gas actually leaves the box is when things change. It will cool off rapidly at that point and many gases could undergo liquefaction or deposition, so you could get some cool effects there. Of course, the pressure in space is also very low, so the gases have to get pretty cold in order for their vapor pressures to drop below ambient.

Additionally, the flow upstream of the throat will be effectively independent of the low pressure outside the box. Once the gas leaves, the flow will rapidly become rarefied, but we need not consider that in determining the actual flow before it actually leaves the box.

Also, does anyone know of any videos that show actual choked-gas flows in progress?

There wouldn't be anything to see. It's just a flowing fluid with no special characteristics other than the fact that it reaches sonic velocity at the location of smallest cross section.

 

[Albertgauss]

Does anything visible happen at the hole (location of smallest cross section) when the gas reaches sonic velocity, or is that all invisible also? Just curious.

 

[boneh3ad]

For most gases, it is invisible. You can view some compressible flow phenomena (such as shock and expansion waves) using techniques called schlieren or shadowgraphy. You can Google that and come up with all sorts of neat pictures. In the case in question here, nothing interesting would show up until after the flow leaves the hole, in which case there would be a series of expansion waves that might be visible with such techniques and a possible shock diamond structure downstream of that.

 

[cjl]

Also, does anyone know of any videos that show actual choked-gas flows in progress?

This one's pretty cool: