Allow me to elaborate on I wrote in post #6.
I've added some attachments that you can click on below for reference.
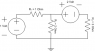
The first attachment shows an example circuit.
The next two attachments show different ways that we've going to solve this problem, using different current loops (same circuit, just different current loops). Assume that we are solving for the voltage across the 3 Ohm resistor.
Solution 1:
Please refer to second attachment, where there are two small loops. We sum together the voltages going around each loop. Since there are two current loops there are two equations:
(-1 V) + (1 \Omega)i_1 + (2 \Omega)(i_1 - i_2) = 0
(2 V) + (3 \Omega)i_2 + (2 \Omega)(i_2 - i_1) = 0
We can re-write each simultaneous equation, simplifying things somewhat,
(1 V) = (1 \Omega)i_1 + (2 \Omega)i_1 - (2 \Omega)i_2
(-2 V) = (3 \Omega)i_2 + (2 \Omega)i_2 - (2 \Omega)i_1
Factor the i_1s in the first equation and the i_2s in the second equation,
(1 V) = (3 \Omega)i_1 - (2 \Omega)i_2
(-2 V) = -(2 \Omega)i_1 + (5 \Omega)i_2
From here, there are a few ways we can go to solve this pair of simultaneous equations. There's linear algebra, substitution, and what I'm going to use here. We're really interested in i_2 since that will give us the voltage across R3. But we need to eliminate i_1 somehow. So let's multiply everything in the top equation by 2 and everything in the bottom equation by 3, in anticipation of adding the two equations together later.
(2 V) = (6 \Omega)i_1 - (4 \Omega)i_2
(-6 V) = -(6 \Omega)i_1 + (15 \Omega)i_2
Now add them together.
(-4 V) = (11 \Omega)i_2
or simply i_2 = -\frac{4}{11} A
which gives us
V_{OUT} = (3 \Omega)(-\frac{4}{11} A) = -\frac{12}{11} V
Solution 2:
We can also solve the problem using totally different current loops. Refer to the third attachment that has one little loop to the left and another big loop that goes all the way around the circuit. The equations for these loops are (starting with the smaller loop):
(-1 V) + (1 \Omega)(i_1 + i_2) + (2 \Omega)i_1 = 0
(-1 V) + (1 \Omega)(i_1 + i_2) + (2 V) + (3 \Omega)i_2 = 0
Simplifying again like before gives us,
(1 V) = (1 \Omega)i_1 + (1 \Omega)i_2 + (2 \Omega)i_1
(-1 V) = (1 \Omega)i_1 + (1 \Omega)i_2 + (3 \Omega)i_2
Factor the i_1s in the first equation and the i_2s in the second equation,
(1 V) = (3 \Omega)i_1 + (1 \Omega)i_2
(-1 V) = (1 \Omega)i_1 + (4 \Omega)i_2
In an attempt to get rid of i_1, we multiply the bottom equation by -3, in anticipation of adding the equations together.
(1 V) = (3 \Omega)i_1 + (1 \Omega)i_2
(3 V) = (-3 \Omega)i_1 + (-12 \Omega)i_2
Now we add the equations together,
(4 V) = (-11 \Omega)i_2
making
i_2 = -\frac{4}{11} A
Thus
V_{OUT} = (3 \Omega)(-\frac{4}{11} A) = -\frac{12}{11} V
Summary:
Different current loops, same answer. Just make sure that each component in the circuit has at least one current loop going through it.
Oh, and you'll make things easier on yourself if you don't create any new current loops containing only components already associated with other loops. In other words, when defining current loops, its best to start with components that don't have any loops associated with them already. Once all the components in the circuit are associated with at least one loop, stop there (and then move on to writing down the simultaneous equations).