How Much Energy Is Needed to Move and Rotate a Weighted Tray Using Rubber Tires?

[Home Improvement]

Hi,

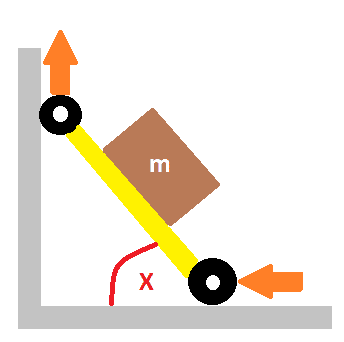
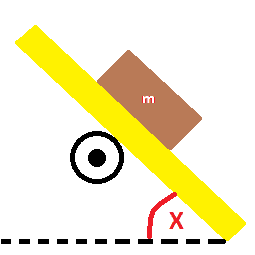
The goal here is to increase/decrease the angle x by 5 degrees. the black circles represent a rubber tire (same as car tires, only smaller), 5cm in diameter, rotating on it's center, powered by a motor. each wheel has 40 psi (2.76 bar) of air in it. the yellow tray on both diagrams are identical, weighing around 20kg and 2m long and 4cm wide. weight (m) on both diagrams are also identical, weighing 200kg, welded shut to the yellow tray.
my questions is I need the formula to calculate the following:
1. in the top diagram, assume front and rear wheels are treading on asphalt surface, so rolling coefficient is around 0.0087. I got this number from https://www.engineeringtoolbox.com/rolling-friction-resistance-d_1303.html. what is the total energy the motor of rear wheel need to exert to move the system from a complete standstill until the increase angle x by 5 degrees?
2. also in the top diagram, I assume the amount of energy exerted would exactly be the same if it's only the front wheel motor that moves?
3. in the bottom diagram, the wheel axis is exactly in the middle of both the weight and the tray. I assume that if x is below 45 degrees, gravity will handle decreasing the angle (motor needs not exert energy to decrease x). the same also applies when angle is above 45 degrees and we want to increase x. if previous assumptions are correct, how much energy does the motor need to exert to decrease x by 5 degrees (when x is greater than 45)? what about increasing x by 5 degrees (when x is less than 45)?
4. for top diagram, I assume we can just rely on gravity if we want to decrease x by 5 degrees? provided that x is not 90 degrees.

thanks

 

[haruspex]

rolling coefficient is around 0.0087

Ok, but what equation turns that into a resistive force?

to move the system from a complete standstill until the increase angle x by 5 degrees?

Please show some attempt. What equations are relevant?

also in the top diagram, I assume the amount of energy exerted would exactly be the same if it's only the front wheel motor that moves?

Interestingly, no. That will become evident if you answer my first question and consider the vertical and horizontal balances of forces.
There is also the matter of whether the tyre against the wall would always have enough friction.

the same also applies when angle is above 45 degrees and we want to increase x

How do you deduce that? Consider potential energy and the way the mass centre will move.

for top diagram, I assume we can just rely on gravity if we want to decrease x by 5 degrees?

Yes, except when close to 90 degrees. There is some rolling resistance to be overcome.

 

[Home Improvement]

Ok, but what equation turns that into a resistive force?

normally, I'd say the weight of object multiplied by coefficient, but since this is rolling, not skidding, not sure which equation to use.

Please show some attempt. What equations are relevant?

sorry, but I just drew a blank. it's been 15 years since I last touched any physics subject. the only equations I got was F = ma and basic torque equation (just guessing it's torque because something is rotating), but not sure how to apply these equations in this system.

Interestingly, no. That will become evident if you answer my first question and consider the vertical and horizontal balances of forces.
There is also the matter of whether the tyre against the wall would always have enough friction.

cant even answer anything

How do you deduce that? Consider potential energy and the way the mass centre will move.

for bottom diagram, now that you mentioned it, when the wheel rotate, even for a bit, the mass center won't be aligned with the center of wheel, meaning, it will always rotate clockwise, meaning, increase x. so, basically, if angle x is greater than 0, the tendency is it will keep increasing, meaning, the motor needs not do any work to increase angle X

Yes, except when close to 90 degrees. There is some rolling resistance to be overcome.

I assume this applies only to top diagram. the system in top diagram will be 5 degrees min and 85 degrees max, so never exactly 0 or 90 degrees. but can you explain how there will be rolling resistance if it's 90 degrees?

 

[haruspex]

the weight of object multiplied by coefficient

More accurately, the normal force multiplied by the coefficient. Both wheels will experience a normal force, so both offer rolling resistance.

the only equations I got was F = ma and basic torque equation

The first step is to draw a free body diagram, showing all the forces on the object, and use force balance and torque balance equations to determine all the forces. (You can treat it as a statics question since you can move very slowly, so acceleration can be ignored.)

if angle x is greater than 0, the tendency is it will keep increasing, meaning, the motor needs not do any work to increase angle X

Yes.

I assume this applies only to top diagram

Both.

can you explain how there will be rolling resistance if it's 90 degrees?

As I noted, it is based on the normal force. At 90 degrees the lower tyre will have maximum normal force, so maximum rolling resistance.