- #1
Swulf
- 2
- 0
I am starting to deal with optomechanical systems as part of my work, and am faced with what seems to be an uncomplicated problem, however I'm ashamed to admit that I am having great difficulty getting to grips with it. I'd like some pointers and/or advice as to how to go about solving these sorts of problems - please note, I want to *learn how to solve them*, I am not just looking for the 'answer'. It's the methods and approaches I want to understand so I can apply it to subsequent problems.
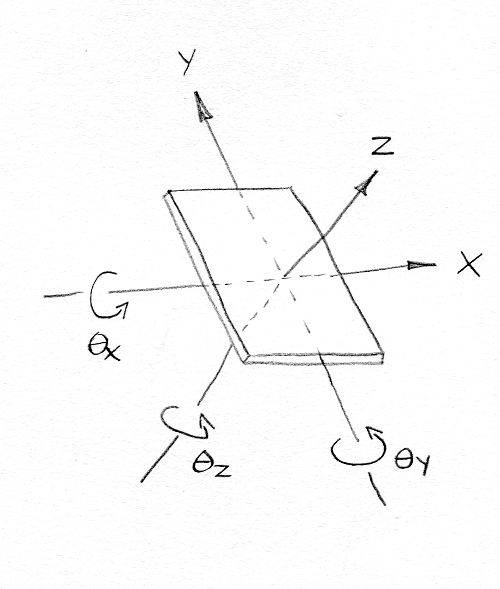
The system I am considering has a flat mirror with axis [itex]X[/itex], [itex]Y[/itex] and [itex]Z[/itex] as shown. Translations in the axial directions are allowed i.e. [itex]\delta X[/itex], [itex]\delta Y[/itex] and [itex]\delta Z[/itex]. Rotations about the axes are also allowed, [itex]\theta_X[/itex], [itex]\theta_Y[/itex] and [itex]\theta_Z[/itex].
The articulated mirror assembly is to sit on another stage which can rotate by an angle [itex]\phi_R[/itex] and can tilt the entire mirror by [itex]\phi_T[/itex]. Obviously [itex]\theta_X = \phi_T[/itex]. The whole thing is intended to steer an incoming beam onto a surface by controlling [itex]\phi_R[/itex] and [itex]\phi_T[/itex] (i.e. [itex]\theta_X[/itex]).
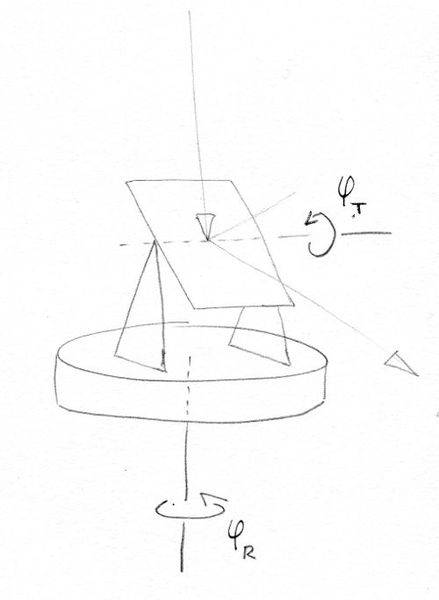
My difficulty in comprehension is how to determine the relationship between [itex]\theta_Y[/itex] and [itex]\phi_R[/itex]. The system will not be able to move in [itex]\theta_Y[/itex], only in [itex]\phi_R[/itex], but some specifications on error have been given in terms of [itex]\theta_Y[/itex] and it is necessary to turn those into corresponding specifications on [itex]\phi_R[/itex]. I am stumped as to how to properly transform between the two. It seems like it should be simple!
I would welcome any advice on how to properly determine the relationship between [itex]\theta_Y[/itex] and [itex]\phi_R[/itex].
Thank you,
Swulf
The system I am considering has a flat mirror with axis [itex]X[/itex], [itex]Y[/itex] and [itex]Z[/itex] as shown. Translations in the axial directions are allowed i.e. [itex]\delta X[/itex], [itex]\delta Y[/itex] and [itex]\delta Z[/itex]. Rotations about the axes are also allowed, [itex]\theta_X[/itex], [itex]\theta_Y[/itex] and [itex]\theta_Z[/itex].
The articulated mirror assembly is to sit on another stage which can rotate by an angle [itex]\phi_R[/itex] and can tilt the entire mirror by [itex]\phi_T[/itex]. Obviously [itex]\theta_X = \phi_T[/itex]. The whole thing is intended to steer an incoming beam onto a surface by controlling [itex]\phi_R[/itex] and [itex]\phi_T[/itex] (i.e. [itex]\theta_X[/itex]).
My difficulty in comprehension is how to determine the relationship between [itex]\theta_Y[/itex] and [itex]\phi_R[/itex]. The system will not be able to move in [itex]\theta_Y[/itex], only in [itex]\phi_R[/itex], but some specifications on error have been given in terms of [itex]\theta_Y[/itex] and it is necessary to turn those into corresponding specifications on [itex]\phi_R[/itex]. I am stumped as to how to properly transform between the two. It seems like it should be simple!
I would welcome any advice on how to properly determine the relationship between [itex]\theta_Y[/itex] and [itex]\phi_R[/itex].
Thank you,
Swulf