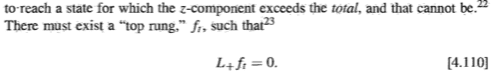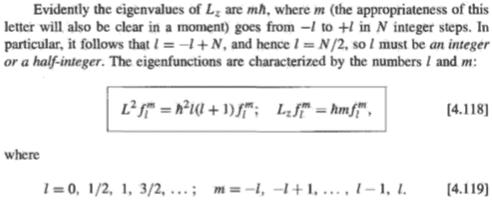I How to be sure we have found all magnetic quantum numbers?

[Happiness]

The book uses ladder operators $L_+$ and $L_-$ to find the eigenvalues $m$ of $L_z$. By first deducing that these operators raise or lower the eigenvalue by $\hbar$, and then deducing that the lowest eigenvalue is the negative of the highest eigenvalue $l$, it proves that $m = -l, -l+1, ... , l-1, l$.

But I suspect these values of $m$ may not be exhaustive, at least not proven to be by this method. This is because the use of these ladder operators is quite arbitrary; there may exist other operators that change the eigenvalue by say $\frac{1}{2}\hbar$ or $\frac{1}{3}\hbar$.

Am I right to say the method of using ladder operators $L_+$ and $L_-$ could not give us all the possible values of $m$?

Reference: Introduction to Quantum Mechanics, David J. Griffiths. p162

 

[hilbert2]

Isn't it geometrically obvious that a component of angular momentum vector can't be longer than the vector itself?

 

[vanhees71]

The key point indeed is that you look for irreducible representations of the Lie algebra su(2) (aka angular momentum operators). This implies that you look for a complete set of orthonormalized vectors spanning the corresponding vector space the representation lives on. To that end you need to specify a complete set of commuting operators, and in the case of su(2) these are $\hat{\vec{J}}^2$ and $\hat{J}_3$ (or any other component, but conventionally one uses the 3-component, as we usually choose the 3-axis as the polar axis of spherical coordinates).

Then the proof is complete: For a given eigenvalue of $\hat{\vec{J}}^2$ the possible eigenvalues for $\hat{J}_z$ are bounded. Further since you look for an irrep the operator algebra (spanned by $\hat{\vec{J}}$) acts transitively on the Hilbert space. Since the ladder operators $\hat{J}_{\pm} = \hat{J}_1 \pm \mathrm{i} \hat{J}_2$ lower and raise the eigenvalues of $\hat{J}_z$ by one unit (in units of $\hbar$ of course), you must have $\hat{J}_+|J,M_{\text{max}} \rangle=0$, because otherwise $M_{\text{max}}+1$ would be an eigenvalue of $\hat{J}_z$, but that contradicts the assumption that $M_{\text{max}}$ is the maxmal possible eigenvalue at in the space of eigenvectors of $\hat{\vec{J}}^2$. This analysis leads to the conclusion that the eigenvalues of $\hat{\vec{J}}^2$ are given by $j(j+1)\hbar^2$ with $j \in \{0,1/2,1,\ldots \}$. Each of this possible values determines uniquely an irrep of su(2), and for each $j$ the eigenvalues of $\hat{J}_3$ are $M \in \{-j,-j+1,\ldots,j-1,j\}$.

 

[Happiness]

I think you guys misunderstood my point. I was saying it’s possible $m=-l, -l+\frac{1}{2}, -l+1, ... , l-1, l-\frac{1}{2}, l$. Just because the ladder operators $L_+$ and $L_-$ find $m$ values that differ from each other by integer amount, it doesn’t preclude, I think, the possibility of the existence of some other operators that could give other $m$ values.

 

[vanhees71]

No that's not possible. The ladder operators action on an eigenstate of $\hat{L}_z$ follows uniquely from the commutation relations of the angular-momentum operators. They thus uniquely change the eigen value by $\pm \hbar$ and NOT by $\pm \hbar/2$!

 

[PeterDonis]

there may exist other operators that change the eigenvalue by say $\frac{1}{2}\hbar$ or $\frac{1}{3}\hbar$.

Remember we are talking about the possible eigenvalues of one operator, $L_z$. So there would have to be operators other than $L_{\pm}$ that would take an eigenstate of $L_z$ with one eigenvalue, and change it to an eigenstate of $L_z$ with another eigenvalue. Call such an operator $X$.

Now work through the same logic that Griffiths goes through, applying $X$ to an eigenstate of $L_z$ and writing down the equation $X$ would have to satisfy in order to change that eigenstate to another one whose eigenvalue differed from the first by something other than $\hbar$. You will see that, as in equation 4.109 in Griffiths, the change in eigenvalue is given by the commutator of $X$ with $L_z$, i.e., $[L_z, X]$. So for an operator $X$ to change the eigenvalue of $L_z$ by something other than $\hbar$, we would have to have $[L_z, X]$ be something other than $\hbar$ (but not zero).

But there can't be any such operator $X$, because any such operator would have to be expressible as a linear combination of $L_x$, $L_y$, and $L_z$, since those operators span the space of possible operators on spin states, and any linear combination of those operators must either commute with $L_z$ or have commutator $\hbar$ with $L_z$. (In fact it should be evident that $L_{\pm}$ themselves span the space of possible such operators that do not commute with $L_z$.)

 

[hilbert2]

I think you guys misunderstood my point. I was saying it’s possible $m=-l, -l+\frac{1}{2}, -l+1, ... , l-1, l-\frac{1}{2}, l$. Just because the ladder operators $L_+$ and $L_-$ find $m$ values that differ from each other by integer amount, it doesn’t preclude, I think, the possibility of the existence of some other operators that could give other $m$ values.

Ok, I misunderstood your point... I thought you meant $m$ values greater than $l$, not values between the known ones.

 

[vanhees71]

Remember we are talking about the possible eigenvalues of one operator, $L_z$. So there would have to be operators other than $L_{\pm}$ that would take an eigenstate of $L_z$ with one eigenvalue, and change it to an eigenstate of $L_z$ with another eigenvalue. Call such an operator $X$.

Now work through the same logic that Griffiths goes through, applying $X$ to an eigenstate of $L_z$ and writing down the equation $X$ would have to satisfy in order to change that eigenstate to another one whose eigenvalue differed from the first by something other than $\hbar$. You will see that, as in equation 4.109 in Griffiths, the change in eigenvalue is given by the commutator of $X$ with $L_z$, i.e., $[L_z, X]$. So for an operator $X$ to change the eigenvalue of $L_z$ by something other than $\hbar$, we would have to have $[L_z, X]$ be something other than $\hbar$ (but not zero).

But there can't be any such operator $X$, because any such operator would have to be expressible as a linear combination of $L_x$, $L_y$, and $L_z$, since those operators span the space of possible operators on spin states, and any linear combination of those operators must either commute with $L_z$ or have commutator $\hbar$ with $L_z$. (In fact it should be evident that $L_{\pm}$ themselves span the space of possible such operators that do not commute with ##L_z.)

In the following I work in natural units with $\hbar=1$.

I don't understand this argument. A ladder operator $\hat{X}$ for $L_z$ eigenstates must have a commutation relation like
$$[\hat{L}_z,\hat{X}]=\lambda \hat{X},$$
because only then
$$\hat{L}_z \hat{X} |m \rangle=([\hat{L}_z,\hat{X}]+\hat{X} \hat{L}_z)|m \rangle=(\lambda +m) \hat{X} |m \rangle,$$
i.e., $\hat{X} |m \rangle$ is eighter 0 or an eigenvector of $\hat{L}_z$ with eigenvalue $m+\lambda$.

Now we want an irrep of the entire Lie algebra su(2) generated by the $\hat{L}_k$. Due to Schur's Lemma this must be an eigenspace of $\hat{\vec{L}}^2$ since $\hat{\vec{L}}^2$ is the only Casimir operator of su(2). From the commutator relations
$$[\hat{L}_j,\hat{L}_k]=\mathrm{i} \epsilon_{jkl} \hat{L}_l$$
it's clear that the operator $\hat{X}$ must be a linear combination,
$$\hat{X}=a \hat{L}_1 + b \hat{L}_2.$$
The commutator with $\hat{L}_z$ is
$$[\hat{L}_z,\hat{X}]=\mathrm{i} (a \hat{L}_2-b \hat{L}_1) \stackrel{!}{=} \lambda (a \hat{L}_1 + b \hat{L}_2).$$
This means
$$a=-\mathrm{i} \lambda b, \quad b=\mathrm{i} \lambda a.$$
This homogeneous system of linear equations can only have non-trivial solutions for $\lambda = \pm 1$, and the corresponding operators are
$$\hat{X}_{\pm}=a (\hat{L}_x \pm \mathrm{i} \hat{L}_y)=a \hat{L}_{\pm}.$$
From only this we can draw the conclusion that ladder operators for $\hat{L}_3$-eigenstates can change the eigenvalues only in steps of $\pm 1$. And the ladder operator must be proportional to the usual ladder operators $\hat{L}_{\pm}$.

Now you have to fulfill also the eigenvalue equation
$$\hat{\vec{L}}^2 |\alpha,m \rangle=\alpha |\alpha,m \rangle,$$
and then you can use the usual argument with $\hat{X}_{\pm}$ as with the $\hat{L}_{\pm}$. Since you have to express $\hat{\vec{L}}^2$ in terms of the $\hat{X}_{\pm}$ and $\hat{L}_z$ the arbitrary constant $a$ is compensated in the solutions for the eigenvalues of the common eigenstates of $\hat{\vec{L}}^2$ and $\hat{L}_z$, namely $\alpha=l(l+1)$ with $l \in \{0,1/2,1,\ldots \}$ and for each $l$, i.e., for each irrep of su(2), $m \in \{-l,-l+1,\ldots,l \}$.

Also note that, if you are after the orbital angular-momentum operators
$$\hat{L}_j=\epsilon_{jkl} \hat{x}_k \hat{p}_l$$,
then you have to prove in addition that here only integer solutions for $l$ are allowed, but that's another story.

 

[PeterDonis]

I don't understand this argument.

It seems to me that you understand it fine, since you just reproduced it in much more detail, more precisely stating some things I stated in a sloppy way, and with proper math and references to the relevant theorems. The key point is that any operator that does not commute with $L_z$ and acts on an eigenstate of $L_z$ to produce another eigenstate, must be proportional to $L_{\pm}$, and must change the eigenvalue by integer steps, which rules out the possibility @Happiness was suggesting.

 

[Vanadium 50]

Just because the ladder operators L+L_+ and L−L_- find mm values that differ from each other by integer amount, it doesn’t preclude, I think, the possibility of the existence of some other operators that could give other mm values.

You can go back to solving the differential equations, and see that these supposed other eigenstates of yours are not solutions.