What is Quantum numbers: Definition and 122 Discussions

In chemistry and quantum physics, quantum numbers describe values of conserved quantities in the dynamics of a quantum system. Quantum numbers correspond to eigenvalues of operators that commute with the Hamiltonian—quantities that can be known with precision at the same time as the system's energy—and their corresponding eigenspaces. Together, a specification of all of the quantum numbers of a quantum system fully characterize a basis state of the system, and can in principle be measured together.
An important aspect of quantum mechanics is the quantization of many observable quantities of interest. In particular, this leads to quantum numbers that take values in discrete sets of integers or half-integers; although they could approach infinity in some cases. This distinguishes quantum mechanics from classical mechanics where the values that characterize the system such as mass, charge, or momentum, all range continuously. Quantum numbers often describe specifically the energy levels of electrons in atoms, but other possibilities include angular momentum, spin, etc. An important family is flavour quantum numbers – internal quantum numbers which determine the type of a particle and its interactions with other particles through the fundamental forces. Any quantum system can have one or more quantum numbers; it is thus difficult to list all possible quantum numbers.

View More On Wikipedia.org
Recent contents Top users
  1. P

    I Exploring the Relationship between Quantum Numbers and Energy in Atomic Systems

    The quantum number n determines the energy, and for each n the allowed values for the angular momentum quantum number are -(n-1),...,(n-1). This doesn't seem resonable to me. Classically increasing the orbital angular momentum will result in an increase in the energy of the system. But why is it...
  2. P

    A Clarifying Fradkin's Terminology on Quantum Numbers of Gauge Groups

    Hi, I'd like to clarify the following terminology (Fradkin, Quantum Field Theory an integrated approach) "carry the quantum numbers of the representation of the gauge group": Does the author basically mean that the wilson loop is a charged operator, in a sense that it transforms non-trivially...
  3. M

    I How are good quantum numbers related to perturbation theory?

    Hello folks, I am currently studying from Griffiths' Introduction to Quantum Mechanics and I've got a doubt about good quantum numbers that the text has been unable to solve. As I understand it, good quantum numbers are the eigenvalues of the eigenvectors of an operator O that remain...
  4. K

    I Good and bad quantum numbers

    Hello! Assume I have a system containing intrinsic spin and orbital angular momentum and before coupling the two, ##|J,J_z,S,S_z,L,L_z>## is a good basis (i.e. all these quantum numbers are good), with ##J=L+S## and ##J_z = S_z + L_z##. If I add a term of the form ##S\cdot L##, ##L_z## and...
  5. A

    I The sum of S and L quantum numbers

    I am reading the textbook Magnetism and Magnetic Materials by Coey and I am confused about how they grouped the terms and how they ended up getting the sums of L and S. My confusion lies in the two red boxes. Also, how is D even considered here when we have up to $2p_1$? And why would the spin...
  6. Decimal

    I Does the Wigner-Eckart theorem require good quantum numbers?

    I have a question related to the following passage in the quantum mechanical scattering textbook by Taylor, Here Taylor makes the choice to use a basis of total angular momentum eigenvectors instead of using the simple tensor product given in the first equation above (6.47). I understand that...
  7. T

    I Quantum numbers for energy levels

    Hello Can some one explain how you work out the combinations of quantum numbers for infinite wells in higher dimensions? For example if i have an energy level $$E_4$$ In a 2D well, then for quantum numbers does this mean the combinations allowed must be: $$4^2 + 1^2$$ $$1^2 + 4^2$$ So then...
  8. jjson775

    Quantum numbers for p-mesons substituted for electrons

    n = 3, l = 2, me = -2, -1, 0, 1, 2. ms = -1 or 1. The correct answer is that ms can also be 0. Why?
  9. A

    Allowed or forbidden reactions

    Hello everybody! I have a doubt about a reaction. $$ p + n \rightarrow \Lambda + \Sigma^+ $$ I have to establish if it is allowed or not. Charge is conserved (1 -> 1) Baryon number is conserved (2 -> 2) Strangeness is not conserved (0 -> -2) Third component of the isospin is not conserved (0...
  10. A

    Quantum numbers of a system of particles

    Hello everybody! I have a problem with this exercise when I have to find the possible angular momentum. Since ##\rho^0 \rho^0## are two identical bosons, their wave function must be symmetric under exchange. $$(exchange)\psi_{\rho\rho} = (exchange) \psi_{space} \psi_{isospin} \psi_{spin} =...
  11. H

    I How to be sure we have found all magnetic quantum numbers?

    The book uses ladder operators ##L_+## and ##L_-## to find the eigenvalues ##m## of ##L_z##. By first deducing that these operators raise or lower the eigenvalue by ##\hbar##, and then deducing that the lowest eigenvalue is the negative of the highest eigenvalue ##l##, it proves that ##m = -l...
  12. S

    Confusion regarding Quantum numbers

    Problem Statement: Given in the "Attempt at a solution section". Relevant Equations: Given in the "Attempt at a solution section". Problem Statement: Given in the "Attempt at a solution section". Relevant Equations: Given in the "Attempt at a solution section". I am having some serious...
  13. Rupul Chandna

    I Why is separation constant l(l+1) instead of +-l^2?

    While separating variables in the Schrodinger Equation for hydrogen atom, why are we taking separation constant to be l(l+1) instead of just l^2 or -l^2, is it just to make the angular equation in the form of Associated Legendre Equation or is there a deeper meaning to it?
  14. P

    Determine fine-structure constant

    Homework Statement The figure below shows the hyperfine structure in the transition 6s $^2S_{1/2}$ - 8p $^2P_{3/2}$ in 115In (I = 9/2). The measurement is made using a narrow-band tunable laser and a collimated atomic beam; hence the Doppler width is greatly reduced. The 6 components shown have...
  15. T

    I Low quantum numbers, high energy, and distance scales.

    I understand how we associate high energies with small wavelengths and thus small distance scales, but we also tend to associate small distance scales with ordinary quantum mechanics, and hence low quantum numbers (low energy). Also, many high-energy processes are active across large distance...
  16. Y

    Orbital/Spin angular momentum + magnetic quantum numbers

    Homework Statement A single electron atom has the outer electron in a 4f1 excited state. Write down the orbital and spin angular momentum quantum numbers and the associated magnetic quantum numbers for this state. Homework Equations I don't think there is any relevant equations. I think it...
  17. Hallucinogen

    B How and why do electron quantum numbers affect bonding?

    Hi, I just have a few questions I'm struggling to find straightforward answers to online. The 4 quantum numbers of an electron in an atom describe the energy level, shape and suborbital of the orbital, and the fourth assigns a value to the electron's spin. Question 1) why is it in lone atoms...
  18. D

    I How Does Rubidium's Electron Spin Affect Its Energy Levels?

    Hello everybody, while I tried to understand the Rubidium level scheme, I realized that I have some issues concerning the energy levels in general... If in addition to the orbital Momentum the spin momentum of an electron is considered for example the p level splits to the 2P1/2-level and the...
  19. N

    I Spin quantum numbers: correct names and formulae?

    I'm having trouble finding the correct names for the 4 standard labels: n, l, m, s. Where might I find, free online: their correct names (ie, no colloquialisms or short cuts) and the accepted formula for each (to be sure I use them correctly)? Thanks.
  20. S

    I Quantum numbers of Landau levels

    I have been reading about Landau levels for a two-dimensional system of charged particles in a perpendicular magnetic field and I have trouble understanding why there is degeneracy in the system. Let me provide some background to my problem. In the presence of a magnetic field, the momentum of a...
  21. Y

    L, m quantum numbers of 3D oscillator

    Homework Statement 6 degenerate energy states at E=7/2 h-bar w in isotropic 3D harmonic oscillator. pick one possible state( for example, (nx,ny,nz)=(1,0,1)), and find possible l, m quantum numbers you may use orthonormality of spherical harmonics[/B] Homework Equations pick one possible...
  22. G

    I Understanding Quantum Numbers and Symmetry Algebra for Keplerian Motion

    so(4) is the symmetry algebra of Keplerian motion. Its structure is well known. The principal quantum number n must be a positive integer. The associated Casimir operator has eingenvalues n^2 - 1 . The secondary quantum number j is integer and can take any value from zero to n-1. The...
  23. Amy B

    I Quantum number and energy levels

    how does the quantum number n in the wavefunction equation for a particle in a 1D box lead to increasingly well-separated energy levels? I know that the separation of energy between the levels is given by ΔE = (2n+1)h^2 / 8mL^2 which means that the higher the n, the greater the energy...
  24. K

    I Quantum numbers - Total Energy and Orbital Momentum

    With the quantum numbers l=1, n=2 and m=-1 how do I calculate the total energy E, L2 (the square of the orbital momentum) and Lz (the z-component of the orbital angular momentum. I've been trying for two hours and am getting no were. Please help
  25. S

    A Exploring the Quantum Numbers of SU(3) Multiplets

    Dear All I just have a question. We say that the SU(2) doublet have the same value of isospin but the particles of this multiplet differs by I3. Now what quantum number the particles of SU(3) multiplet share. Thank you
  26. Tabasko633

    2D Harmonic Oscillator Quantum numbers

    Homework Statement In the exercise, we solved the 2D Harmonic Oscillator in kartesian (x,y) and polar (r,φ) coordinates. We found out that both have the same energy levels, but they look very different, when I plot them. What am I missing? The polar solution seems more like it. Homework...
  27. kalimaa

    A Relationship between Quantum Numbers and Quantum Information

    I would appreciate any clarification (or opinion) on the relationship between Quantum Numbers and Quantum Information. My question is related to the puzzle wether matter merely represents information or - at the basement level of reality - actually can be said to be information. Just to give...
  28. U

    What are the quantum numbers (n, L, J)?

    Homework Statement [/B] I'm supposed to find the quantum numbers (n, L, J) for the first 3 energy levels in Iridium (Z=77), given that the first 4 ionization energies are ##76.1, 13.4, 12.8, 11.2 keV##. Homework EquationsThe Attempt at a Solution I know that the electronic configuration is...
  29. R

    Determining electron configuration with quantum numbers n l

    This relates to a question I asked recently on Quantum Dots, but I'll rephrase it and hopefully any chemists out there can help. If we have (n,l) = (1,2) where n and l are quantum numbers can we determine the orbitals? and hence the number of electrons in a quantum dot? i.e. And also I've...
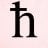
  30. HiggsBoson1

    Understanding Quantum Numbers: Exploring Half Integers and Their Limitations

    I don't understand why quantum numbers can not be divided into half integers and so on. The books I have read do not give clear explanations. Would anyone mind helping me understand this? Thanks!
  31. H

    Principle and Angular Momentum Quantum Numbers

    My understanding of the angular momentum quantum number is that a different number indicates a different region of space that the electron can occupy. So does the principle quantum number determine the size of that region? For example, is 2s the same as 3s in shape, but the 3s has a greater...
  32. TrickyDicky

    Is SU(2) the key to understanding quantum numbers and symmetry?

    Is it purely coincidental that the internal symmetry related flavor quantum numbers(like isospin and weak isospin) and the spacetime symmetry related spin quantum number have SU(2) as underlying group? They refer to seemingly unrelated things but it is remarkable how ubiquitous SU(2) is.
  33. R

    What is the internal and external quantum numbers of a atom

    I am reading a book about the interaction between atom and photon. I don't understand the following statement: "for the sake of simplicity, we assume the atom to be infinitely heavy and disregard the external quantum numbers" Q: what is the external (or internal) quantum number of an atom.
  34. J

    What are the quantum numbers of the Higgs boson?

    Hi everyone, I have studied QFT, the SM and the Higgs mechanism when I was in university and after reading an article from CMS (CERN) about the spin-parity measurement of the HZZ channel, which shows that J^{P}=0^+ is favoured versus J^{P}=0^-, I went back to the theory of the Higgs boson...
  35. Feodalherren

    Quantum Numbers: Why (3,-2,0,1/2) is Invalid

    Homework Statement Why isn't (3, -2 , 0 , 1/2) a valid quantum number? Homework Equations The Attempt at a Solution n=3 so l = -2 is valid. -l≤Ml≤l 2≤Ml≤-2 nonsensical statement. I don't know what to do...
  36. D

    Parition function for Boson gas with two quantum numbers

    Parition function for Boson "gas" with two quantum numbers Let's say that we have a system of non-interacting Bosons with single-particle energies given by, \epsilon_{p,m} = \frac{p^2}{2m} + \alpha m where m = -j, ... ,j and we want to calculate the partition function of this...
  37. B

    Archived Orbital Quantum Numbers And Total Electron Energy

    Hello :smile: Homework Statement The orbital quantum number for the electron in the hydrogen atom is l = 4. What is the smallest possible value (in eV) for the total energy of this electron? (Use the quantum mechanical model of the hydrogen atom.) Homework Equations The Attempt at a Solution...
  38. C

    Understanding K Mixing Level, K Selectivity and K Quantum Numbers

    Can someone explain in simple terms "K mixing level" and "K selectivity" in nuclear decay processes ? ...as it relates to the "K quantum number". And does it relate directly to the nuclear angular momentum?...and selection rules? How so? Dumb it down for me please. Thank you kindly.
  39. D

    Allowed combinations of remaining quantum numbers when n = 3

    Homework Statement Hey everyone I couldn't really fit a good description into the title. Basically here's what it is. Consider an atom in which all the states with principal quantum number n = 3 and angular momentum quantum number l = 2 are occupied by electrons (this is called a closed...
  40. A

    Finding Quantum numbers from wavefunction

    Homework Statement Consider a spinless particle in a central field in a state described by: \psi_a(r) = (x^2 - y^2) e^{-\alpha r^2} \psi_b(r) = xyz e^{-\alpha r^2} Find quantum numbers l and l_z (or their appropriate superposition) for these two cases. Homework Equations...
  41. A

    Four quantum numbers problem

    Homework Statement Give a possible set of values of the four quantum numbers for all the electrons in boron atom and a nitrogen atom if each is in the ground state. I know the principles behind this. It comes from Zumdahl's Chemistry textbook (ninth edition, p. 345, number 95). The...
  42. Q

    Quantum Numbers and Valence Electrons

    Homework Statement 1) Apparently it's a true statement that the quantum numbers 2, 0, 0, 1/2 can apply to any of Cl's electrons. But chlorine's electron configuration is [Ne]3s^2 3p^5. What happened to the n = 3 electrons? 2) How many valence electrons can a ground state oxygen atom have...
  43. H

    Clarification on J and F (total angular momentum quantum numbers)

    Homework Statement I am to consider the Zeeman Effect. I need to calculate the energy level shifts for a given magnetic field corresponding to different quantum numbers. I'm having a hard time knowing when a quantum number Q should be interpreted as just Q or as (Q, Q-1, ..., 0, ..., -Q)...
  44. S

    What do the Ms in ml and ms quantum numbers stand for?

    I first thought magnetic, but that only makes sense for ml, they're both projections though, does anyone know what they stand for? Thanks!
  45. lonewolf219

    How to determine quantum numbers for beta functions?

    I'm trying to understand the notation (3, 1, 2/3) for the up quark and (3, 2, 1/6) for the left-handed up and down quarks... Is the first number related to SU(3), the second SU(2) and the third I believe is the hyper charge... Not sure what the significance is of the first two numbers... I...
  46. S

    HUP and good quantum numbers that commute

    I have a question about the HUP. As I understand the HUP, it only applies to conjugate attributes that do not commute, such as position and momentum. However, many good quantum numbers do commute, so does this mean that the HUP does not apply to simultaneous measurement of such good quantum...
  47. DiracPool

    What is the relationship between angular momentum and energy in electrons?

    I'm a little fuzzy on the meaning of the angular momenta in electrons. From my understanding, the orbital angular momentum of an electron can have integer values of h-bar and the intrinsic "spin" can be 1/2 (and both can be positive or negative). How does this relate to the energy of the...
  48. Mandelbroth

    Deriving Quantum Numbers from the Schrodinger Equation

    Can someone explain to me how one gets the values of n, l, and ml (principle quantum number, azimuthal quantum number, magnetic quantum number, respectively) from the Schrodinger equation for use in chemistry involving distribution of electrons in a hydrogen atom?
  49. dbmorpher

    What Are Quantum Numbers and How Are They Calculated?

    I have read many sources about quantum numbers and I know they have to do with the spin or types of particles in a hadron or boson, but I do not understand how spin could calculated or what it means. There was also something that had symbols that were like, p2, k4, f3... I just don't understand...
  50. N

    Quantum Mechanics and Electron Configuration in a Modified Universe

    Homework Statement In a universe different from ours, the laws of quantum mechanics are the same as ours with one small change. In this different universe the m ℓ quantum number obeys this rule. mℓ = (-ℓ-1), (-ℓ),..,0,...(ℓ), (ℓ+1) In this different universe, what is the maximum number...
Back
Top