- #1
Lensmonkey
- 10
- 0
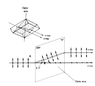
I am trying to calculate what thickness of LiNbO3 would displace a beam of light 9 microns. I seek to make something like a microscope slide that would displace light in the vertical. I am confused about something else if someone can clarify; for the crystal, I think the "z" axis is "optical axis." I think from what I have read that light that travels this axis in any polarization is unaffected, Is this correct? If so it confuses specifying the dimensions of the slide, as I think of the z dimension as being the thickness. A "z-cut" crystal in this case would not displace at all would it?