- #1
yeyintkoko
- 16
- 0
1. Homework Statement
if δ=7.7 %; Pm=0.2349 and
if δ=30.8 %; Pm=0.9180.
2. Homework Equations
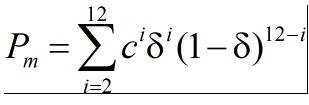
We can calculate value of c if we know value of Pm and δ? Please help me.
Thanks You![/B]
if δ=7.7 %; Pm=0.2349 and
if δ=30.8 %; Pm=0.9180.
2. Homework Equations
The Attempt at a Solution
We can calculate value of c if we know value of Pm and δ? Please help me.
Thanks You![/B]