akmphy
- 16
- 0
HELP with thin film problem!
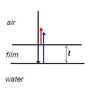
Consider a horizontal plane of thin film with
a thickness t. This film is located in between
air and water (see sketch). Light is directed
from the air downward through the film and
into the water, perpendicular to the surfaces.The index of refraction of the film n1 = 1.5.
The index of refraction of water is n2 = 1.33.
The wavelength of the incident wave in the air
is lambda air, and its frequency in air is f =
c/
.The wavelength lambda water of the light in the
water is:
and The smallest non-zero thickness t(min) leading
to no reflection is:
t= m(lambda film)/2
I know the net phase change equals one half of the wavelength because it undergoes a phase change from air to film, and experiences no phase change from film to water. I do not understand how to start this problem. I thought that the wave would reflect off the surface of the water, thus experiencing no wavelength in the water. Any help would be appreciated. No, I have no idea how to attach the image. It is three parallel surfaces, with n1 being the film, and n2 being the water
Homework Statement
Consider a horizontal plane of thin film with
a thickness t. This film is located in between
air and water (see sketch). Light is directed
from the air downward through the film and
into the water, perpendicular to the surfaces.The index of refraction of the film n1 = 1.5.
The index of refraction of water is n2 = 1.33.
The wavelength of the incident wave in the air
is lambda air, and its frequency in air is f =
c/
.The wavelength lambda water of the light in the
water is:
and The smallest non-zero thickness t(min) leading
to no reflection is:
Homework Equations
t= m(lambda film)/2
The Attempt at a Solution
I know the net phase change equals one half of the wavelength because it undergoes a phase change from air to film, and experiences no phase change from film to water. I do not understand how to start this problem. I thought that the wave would reflect off the surface of the water, thus experiencing no wavelength in the water. Any help would be appreciated. No, I have no idea how to attach the image. It is three parallel surfaces, with n1 being the film, and n2 being the water