lussi
- 14
- 0
Homework Statement
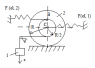
A mechanical system consists of body 1, having mass m1 = 54 kg, a two-stage disc 2, having mass m2 = 24 kg and radii R = 0.6 m and i = R/4 (i is the radius of inertia about the central axis, perpendicular to the disc), and two equal horizontal linear springs, each of the of a coefficient of elasticity c = 1092 N/m. A non-elastic cord of negligible mass rolled over the small stage connects the disc with body 1. The disc moves without sliding over a horizontal plane. At the initial instant body 1 is shifted down at x0 = 0.07 m and released without initial velocity. Assuming the system makes small oscillations around its equilibrium, find the differential equation of the system motion (using axis x), find the motion law x(t) and determine the natural frequency as well as the period of these oscillations. (I have attached a picture of the system)
2. Question
I don't want the solution to the whole problem, I just wanted to ask if someone could explain to me how do we take the value of ω2 with respect to the velocity of body 1, with respect to the velocity of point B and C as well. I have the equations, but I don't understand them.
In the book is written:
ω2 = V1 / (R - R/2) = 2V1 / R (why do we subtract the 2 radii)
Vc = ω2*R = 2V1 (why do we multiply by the radius of the big disc)
Vb = ω2*(3R/2) = 3V1 (why do we add the 2 radii)
where V1 is used as the first derivative of x (x with a point on top of it).
Since both, the cord and spring 2 are connected to the smaller disc, shouldn't their velocities be the same?
Attachments
Last edited: