ramialsaiad
- 24
- 0
Hi
I want to calculate the potential energy of the following figure in function of x
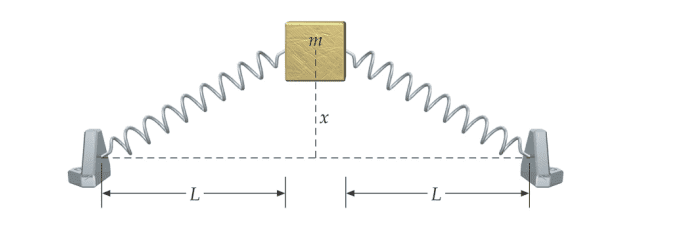
Here is my attempt :
mgx + 1/2*k*(sqrt(x^2+L^2)-L)=1/2*m*v^2
Is that correct ?
thanks
I want to calculate the potential energy of the following figure in function of x
Here is my attempt :
mgx + 1/2*k*(sqrt(x^2+L^2)-L)=1/2*m*v^2
Is that correct ?
thanks
Last edited by a moderator: