- #1
O_o_O_o_O
- 3
- 0
Hi,
I´ve tried to calculate the vibration modes of beam in the space, without gravity or any other force.
The forumle of the beam is this one: Cos(λL)*Cosh(λL)=1 from which I´ve calculate the roots and the resonance.
I´ve found a programme for Matlab that calculates the vibrations modes if you enter the mass and stiffness matrix but it´s here where I´m facing some troubles. I don´t know how to build the stiffnes matrix of this beam.
For the mass matrix I´m going to use this methog. Do you know if it´s going to work properly?
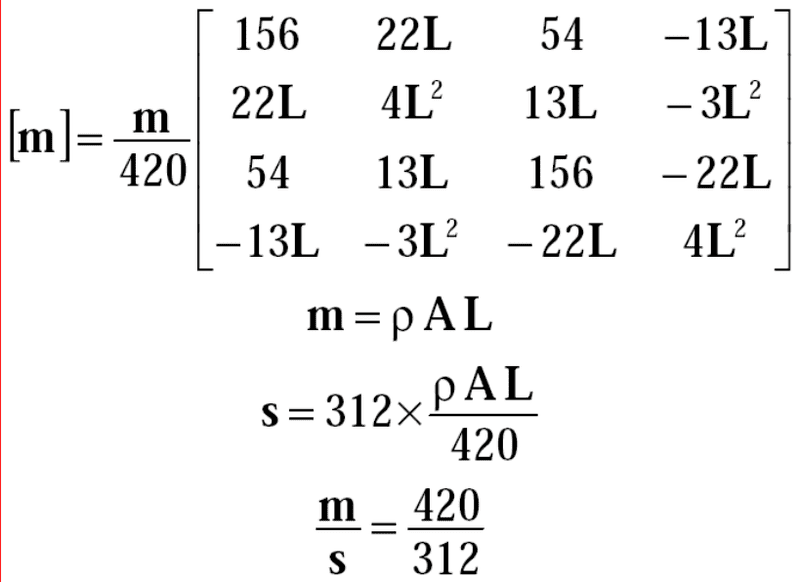
I´ve all the dimensions, density and the young´s modulus of the material (steel).
Thanks in advance.
I´ve tried to calculate the vibration modes of beam in the space, without gravity or any other force.
The forumle of the beam is this one: Cos(λL)*Cosh(λL)=1 from which I´ve calculate the roots and the resonance.
I´ve found a programme for Matlab that calculates the vibrations modes if you enter the mass and stiffness matrix but it´s here where I´m facing some troubles. I don´t know how to build the stiffnes matrix of this beam.
For the mass matrix I´m going to use this methog. Do you know if it´s going to work properly?
I´ve all the dimensions, density and the young´s modulus of the material (steel).
Thanks in advance.