How to calculate this probability (conditional distributions)

[Drao92]

fXY(x,y)=2 if 0<x<1 and x<y<1, 0 for other intervals
I have to calculate: P((x>0.5)π(y<0.5)).
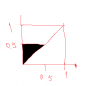
I think it 0 but I am not sure because in all other exercises I've made the surfaces intersect each other. Like in fig 1 for P((x<0.5))π(y<0.5))=integral from 0 to 0.5 from integral from x to 0.5 from 2dydx.
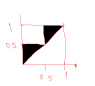
The fig 2 is for P((x>0.5)π(y<0.5)).
Im sorry because i forgot to mark the axis. vertical is y and horizontal is x.I apologize.
https://www.physicsforums.com/attachment.php?attachmentid=58161&stc=1&d=1366802927
https://www.physicsforums.com/attachment.php?attachmentid=58162&stc=1&d=1366802927

 

[mathman]

If I understand your description, the density function = 0 for x > y. Therefore P((x > 0.5) and (y < 0.5)) = 0.