How to calculate transfer function when there is a transformer

[Bromio]

Homework Statement

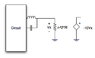
Calculate the transfer function, H(s) = Vo(s)/V1(s), of the given circuit.

The Attempt at a Solution

I see there is an inverting amplifier with gain A = -10. However, I don't know how to complete the analysis with this ideal transformer. How can I substitute it?

Thank you.

 

[NascentOxygen]

With a tightly-coupled transformer, the voltage on the n side is n times the voltage on the 1 side. And because transformers can't invent energy out of thin air, the current on the n side must be 1/n times the current on the 1 side so that power is conserved and P_in = P_out. This means transformers really transform impedances, by a ratio n².

Each side sees the impedance of the circuit connected to the winding on the other side--but transformed by a factor of n² or 1/n² (depending on the side).

 

[Bromio]

And what about impedances in op-amp? Do I multiply it by n^2 too?

 

[NascentOxygen]

Can transform only the Thevenin impedances seen on each side. What the transformer doesn't see, it can't transform.

You might find it easier to do the transform of current and voltage yourself, and not consider impedance being transformed. (You only do one or the other: either transform the impedance from one side to the other, OR adjust the current and voltage by a factor of n or 1/n, respectively. You don't do both.)

So i_out of stage 1 becomes n.i_out = i_in of stage 2.

 

[Bromio]

So, the circuit should look like in the attached figure, shouldn't it?

I don't understand how to modify voltages and currents. I think Vin (stage 2) will have a value of n*Vout (stage 1). Therefore, I'll have to use a controlled voltage source. However, what about current? Do I have to use a controlled current source too?

Thank you.

 

[uart]

So, the circuit should look like in the attached figure, shouldn't it?

I don't understand how to modify voltages and currents. I think Vin (stage 2) will have a value of n*Vout (stage 1). Therefore, I'll have to use a controlled voltage source. However, what about current? Do I have to use a controlled current source too?

Thank you.

Close but not quite correct. The LHS is correct but Vx still needs to be referred to the other side of the transformer before the RHS of your equivalent is correct.

 

[Bromio]

... Vx still needs to be referred to the other side of the transformer before the RHS of your equivalent is correct.

I don't understand how to do what you are saying? Could you explain it again?

Thank you.

 

[rude man]

Questions you should ask yourself:
1. what is the load impedance on the secondary?
2. what does that do to the voltage divider formed by your L-C network and the reflected impedance at the transformer primary?
3. what's the voltage ratio between the primary & the secondary?

The rest should be obvious.

PS - I don't recommend using controlled sources in your equivalent circuit. Better to use the fundamental properties of an ideal transformer.

 

[Bromio]

Questions you should ask yourself:
1. what is the load impedance on the secondary?

The load impedance on the secondary is R.

2. what does that do to the voltage divider formed by your L-C network and the reflected impedance at the transformer primary?

Should I analyze the voltage divider formed by the LC network and a resistor with value n^2*R?

3. what's the voltage ratio between the primary & the secondary?

V1 = n*V2.

When I substitute the resistor and the transformer by n^2*R, which is the voltage in n^2*R, ¿V1 = n*V2?

Thank you.

 

[NascentOxygen]

So, the circuit should look like in the attached figure, shouldn't it?

I don't understand how to modify voltages and currents. I think Vin (stage 2) will have a value of n*Vout (stage 1). Therefore, I'll have to use a controlled voltage source. However, what about current? Do I have to use a controlled current source too?

Thank you.

You have the equivalent circuit for the left hand side correct, so analyse it as though it's a standalone circuit and determine Vx and Ix.

Now that that's done, turn to the op amp. You are using an ideal transformer, both current and voltage are transformed exactly. So the op-amp's input resistor sees a voltage of V_x/n and its current is n.I_x

 

[rude man]

The load impedance on the secondary is R. RIGHT.


Should I analyze the voltage divider formed by the LC network and a resistor with value n^2*R? YES!


V1 = n*V2. I WOULD HAVE SAID, V(secondary) = V(primary)/n. You need V(secondary) to finish, right?

Then don't forget the op amp stage gain ...

 

[Bromio]

Thank you.

So, the voltage drop in n^2*R is Vx and the gain in the ap-omp stage is Vo = -10*Vx/n.

Is it correct?

I think another solution would have been to multiply L and C by 1/n^2 and the input voltage by 1/n, right?

 

[NascentOxygen]

Thank you.

So, the voltage drop in n^2*R is Vx and the gain in the ap-omp stage is Vo = -10*Vx/n.

Is it correct?

Yes...though I'd phrase it as the voltage across ...

I think another solution would have been to multiply L and C by 1/n^2 and the input voltage by 1/n, right?

Try it and see whether you get the same answer.

 

[Bromio]

Thank you.

I've got the same answer!

 

[NascentOxygen]

I've got the same answer!

Then something's wrong.

 

[rude man]

I'm going to give you the answer, since you've worked at it quite a bit:

Vo/Vi = -10(sC + 1/sL)/n(sC + 1/sL + 1/n^2*R)

= -10[(s^2)LC + 1]/n[(s^2)LC + sL/(n^2*R) + 1]

Tip: when dealing with parallel components like your L-C network it's easier to deal with admittances and conductances than with impedances and resistances. That's how my first equation above came about.

BTW the sign is determined by whether the dotted ends of the xfmr are adjacent or not. The minus sign assumes they are. The schematic should have shown this.


NascentO2, did you get the same thing?